Крутящий момент

Теория

В нашей статье по «выбору лучшего шуруповерта» мы уже касались этой темы, но сейчас расскажем чуть подробнее, но так, чтобы ни у кого не закипела голова от формул.

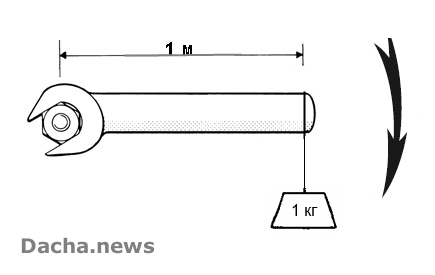
Основным показателем мощности шуруповерта является вращающий момент (крутящий момент), который измеряется в Н·м. Образно говоря, 10 Н·м будет эквивалентен вращающей силе, создаваемой гирей в один килограмм, закрепленной на рычаге в один метр, другой конец которого жестко прикреплен к вращаемому валу.

Для полупрофессиональных моделей шуруповертов, а также предназначенных для домашних мастеров, типичное значение крутящего момента составляет от 10 до 60  Н·м. Если брать «среднюю температуру по больнице», то можно аккуратно предположить, что некий средний шуруповерт имеет характеристику крутящего момента в 25 Н·м.

Однако тут не все так просто, поскольку на практике выдаваемое значение крутящего момента у электромоторов не постоянно и зависит, в первую очередь, от оборотов – чем выше обороты, тем ниже момент на валу. В идеале график линейный с небольшим наклоном – самый низкий момент будет на максимальных оборотах, самый высокий – при неподвижном вале. Но в последнем случае возникнет ситуация, фактически, короткого замыкания обмоток электромотора. За сколько секунд сгорит мотор, зависит от того, из чего сделаны его обмотки. Но будьте уверены, дым и запах гари будут вам обеспечены.

Чтобы не доводить до «греха», дорогие модели имеют систему автоматического отключения при перегрузке, когда соотношение количества оборотов в секунду по отношению к потребляемому току вдруг превысит опасный порог. Однако у нас тут вопрос совсем в другом – какова грань, за которую переходить нельзя, т.е каковы минимальные обороты двигателя, а, следовательно, крутящий момент, при котором он будет работать без перегрева и дальнейшего ущерба для самого себя?

Иными словами, мы уже оперируем двумя значениями крутящего момента. Как вы думаете, какой из них указывается производителем в технических характеристиках шуруповерта? Нет, не угадали. У каждого производителя своя методика измерения и свое понятие об этой характеристике. Деталей никто не раскрывает, и общего стандарта не существует. Потому очень часто можно наблюдать ситуацию, когда более слабый по характеристикам шуруповерт оказывается заметно мощнее более сильного.

Выходом из этой ситуации могут быть только практические испытания в одинаковых условиях.

Расчет мощности двигателя: методики и необходимые формулы

Мощность движка — это энергия, которая образуется внутри ДВС во время его работы. Этот показатель является ключевым для любого автомобиля, а при выборе машины на него ориентируется многие автомобилисты. Определить его можно различными способами. Перечислим основные методики:

• Через обороты и крутящий момент.
• По объему ДВС.
• По расходу воздуха.
• По массе и времени разгона до 100 километров в час.
• По производительности впрыскивающих форсунок.

Главной единицей измерения мощности являются ватты, однако иногда этот показатель выражают с помощью лошадиных сил. Между этими единицами измерения есть простая зависимость, поэтому при необходимости, лошадиные силы, можно легко преобразовать в ватты (и наоборот).

В нашей статье, мы рассмотрим основные формулы определения мощности, а также узнаем, как перевести лошадиные силы в ватты.

Особые случаи и другие факты

Формула руки момента

Схема руки момента

Очень полезный частный случай, который часто называют определением крутящего момента в других областях, помимо физики, выглядит следующим образом:

τзнак равно(момент рука)(сила).{\ displaystyle \ tau = ({\ text {момент руки}}) ({\ text {force}}).}

Конструкция «плеча момента» показана на рисунке справа вместе с векторами r и F, упомянутыми выше. Проблема с этим определением заключается в том, что оно дает не направление крутящего момента, а только его величину, и, следовательно, его трудно использовать в трехмерных случаях. Если сила перпендикулярна вектору смещения r , плечо момента будет равно расстоянию до центра, а крутящий момент будет максимальным для данной силы. Уравнение для величины крутящего момента, возникающего от перпендикулярной силы:

τзнак равно(расстояние до центра)(сила).{\ displaystyle \ tau = ({\ text {расстояние до центра}}) ({\ text {force}}).}

Например, если человек прикладывает усилие 10 Н к концу гаечного ключа длиной 0,5 м (или усилие 10 Н точно на 0,5 м от точки закручивания гаечного ключа любой длины), крутящий момент будет 5 Нм — при условии, что человек перемещает ключ, прикладывая силу в плоскости движения и перпендикулярно ключу.

Крутящий момент, вызванный двумя противоположными силами F _g и -F _g, вызывает изменение углового момента L в направлении этого крутящего момента. Это вызывает прецессию вершины .

Статическое равновесие

Чтобы объект находился в статическом равновесии , не только сумма сил должна быть равна нулю, но и сумма крутящих моментов (моментов) относительно любой точки. Для двумерной ситуации с горизонтальными и вертикальными силами сумма требуемых сил составляет два уравнения: Σ H = 0 и Σ V = 0, а крутящий момент — третье уравнение: Σ τ = 0. То есть для статического решения Для детерминированных задач равновесия в двух измерениях используются три уравнения.

Полезная сила в зависимости от крутящего момента

Когда чистая сила, действующая на систему, равна нулю, крутящий момент, измеренный из любой точки пространства, одинаков. Например, крутящий момент на токоведущей петле в однородном магнитном поле одинаков независимо от вашей точки отсчета. Если результирующая сила не равна нулю и является крутящим моментом, измеренным от , то крутящий момент, измеренный от …
F{\ displaystyle \ mathbf {F}}τ1{\ displaystyle {\ boldsymbol {\ tau}} _ {1}}р1{\ displaystyle \ mathbf {r} _ {1}}р2{\ displaystyle \ mathbf {r} _ {2}}τ2знак равноτ1+(р1-р2)×F{\ displaystyle {\ boldsymbol {\ tau}} _ {2} = {\ boldsymbol {\ tau}} _ {1} + (\ mathbf {r} _ {1} — \ mathbf {r} _ {2}) \ times \ mathbf {F}}

Определение, общие сведения

В физике момент силы играет роль вращающего воздействия на тело.

Видеоурок: вращающий момент

В простейшем случае, если сила F→{\displaystyle {\vec {F}}} приложена к рычагу перпендикулярно ему и оси вращения, то момент силы определяется как произведение величины F{\displaystyle F} на расстояние x{\displaystyle x} от места приложения силы до оси вращения рычага, называемое «плечом силы»:

M=force⋅forcearm=Fx{\displaystyle M=\cdot =Fx}.

Например, сила в 3 ньютона, приложенная на расстоянии 2 м от оси, создаёт такой же момент, что и сила в 1 ньютон с плечом 6 м.

Если действуют две силы, говорят о моменте пары сил (такая формулировка восходит к трудам Архимеда). При этом равновесие достигается в ситуации F1x1=F2x2{\displaystyle F_{1}x_{1}=F_{2}x_{2}}.

Для случаев более сложных движений и более сложных объектов, определение момента как произведения Fx{\displaystyle Fx} требует универсализации.

Момент силы иногда называют вращающим или крутящим моментом. «Вращающий» момент понимается в технике как внешнее усилие, прикладываемое к объекту, а «крутящий» — как внутреннее, возникающее в самом объекте под действием приложенных нагрузок (этим понятием оперируют в сопромате).

Момент силы относительно точки

Момент силы, приложенный к гаечному ключу. Направлен от зрителя

В общем случае, момент силы F→{\displaystyle {\vec {F}}}, приложенной к телу, определяется как векторное произведение

M→=r→×F→{\displaystyle {\vec {M}}=\left},

где r→{\displaystyle {\vec {r}}} — радиус-вектор точки приложения силы. Вектор M→{\displaystyle {\vec {M}}} перпендикулярен векторам r→{\displaystyle {\vec {r}}} и F→{\displaystyle {\vec {F}}}.

Начало отсчета радиус-векторов O может быть любым. Обычно O выбирают в чем-либо выделенной точке: в месте закрепления подвеса, в центре масс, на оси вращения и т.д.. Если одновременно анализируется момент импульса тела L→{\displaystyle {\vec {L}}}, то начало O всегда выбирается одинаковым для L→{\displaystyle {\vec {L}}} и M→{\displaystyle {\vec {M}}}.

Если не оговорено иное, то «момент силы» — это момент силы относительно точки (O), а не некоей оси.

В случае нескольких приложенных сосредоточенных сил их моменты векторно суммируются:

M→=∑ir→i×F→i{\displaystyle {\vec {M}}=\sum _{i}\left},

где r→i{\displaystyle {\vec {r}}_{i}} — радиус-вектор точки приложения i{\displaystyle i}-й силы F→i{\displaystyle {\vec {F}}_{i}}. В случае силы, распределённой с плотностью dF→dV{\displaystyle d{\vec {F}}/dV},

M→=∫Vr→×dF→dVdV{\displaystyle {\vec {M}}=\int \limits _{V}\leftdV}.

Если dF→dV{\displaystyle d{\vec {F}}/dV} (Н/м3) — обобщённая функция, которая может содержать и дельтаобразные члены, то последней формулой охватываются и две предыдущие.

Момент силы относительно оси

Моментом силы относительно оси называется алгебраическое значение проекции момента M→{\displaystyle {\vec {M}}} на ось, то есть

M∥=M→⋅e→o{\displaystyle M_{\parallel }={\vec {M}}\cdot {\vec {e}}_{o}},

где e→o{\displaystyle {\vec {e}}_{o}} — единичный вектор вдоль оси, а начало отсчёта O выбрано на оси. Момент силы относительно оси может быть рассчитан как

M∥=±|r→⊥×F→⊥|{\displaystyle M_{\parallel }=\pm \left|{\vec {r}}_{\perp }\times {\vec {F}}_{\perp }\right|},

где через r→⊥{\displaystyle {\vec {r}}_{\perp }} и F→⊥{\displaystyle {\vec {F}}_{\perp }} обозначены составляющие радиус-вектора и силы в плоскости, перпендикулярной оси.

В отличие от момента силы M→{\displaystyle {\vec {M}}}, величина момента силы относительно оси M∥{\displaystyle M_{\parallel }} не претерпевает изменения при сдвиге точки O вдоль оси.

Для краткости, символ параллельности и знак могут опускаться, а M∥{\displaystyle M_{\parallel }} (как и M→{\displaystyle {\vec {M}}}) именоваться «моментом силы».

Единицы измерения

Момент силы имеет размерность «сила, умноженная на расстояние» и единицу измерения ньютон-метр (джоуль) в системе СИ. 1 Н·м — это момент, который производит сила 1 Н на рычаг длиной 1 м, приложенная к концу рычага и направленная перпендикулярно ему.

Размерность M→{\displaystyle {\vec {M}}} совпадает с размерностями энергии и механической работы.

Определение, общие сведения

В физике момент силы играет роль вращающего воздействия на тело.

Видеоурок: вращающий момент

В простейшем случае, если сила F→{\displaystyle {\vec {F}}} приложена к рычагу перпендикулярно ему и оси вращения, то момент силы определяется как произведение величины F{\displaystyle F} на расстояние x{\displaystyle x} от места приложения силы до оси вращения рычага, называемое «плечом силы»:

M=force⋅forcearm=Fx{\displaystyle M=\cdot =Fx}.

Например, сила в 3 ньютона, приложенная на расстоянии 2 м от оси, создаёт такой же момент, что и сила в 1 ньютон с плечом 6 м.

Если действуют две силы, говорят о моменте пары сил (такая формулировка восходит к трудам Архимеда). При этом равновесие достигается в ситуации F1x1=F2x2{\displaystyle F_{1}x_{1}=F_{2}x_{2}}.

Для случаев более сложных движений и более сложных объектов, определение момента как произведения Fx{\displaystyle Fx} требует универсализации.

Момент силы иногда называют вращающим или крутящим моментом. «Вращающий» момент понимается в технике как внешнее усилие, прикладываемое к объекту, а «крутящий» — как внутреннее, возникающее в самом объекте под действием приложенных нагрузок (этим понятием оперируют в сопромате).

Момент силы относительно точки

Момент силы, приложенный к гаечному ключу. Направлен от зрителя

В общем случае, момент силы F→{\displaystyle {\vec {F}}}, приложенной к телу, определяется как векторное произведение

M→=r→×F→{\displaystyle {\vec {M}}=\left},

где r→{\displaystyle {\vec {r}}} — радиус-вектор точки приложения силы. Вектор M→{\displaystyle {\vec {M}}} перпендикулярен векторам r→{\displaystyle {\vec {r}}} и F→{\displaystyle {\vec {F}}}.

Начало отсчета радиус-векторов O может быть любым. Обычно O выбирают в чем-либо выделенной точке: в месте закрепления подвеса, в центре масс, на оси вращения и т.д.. Если одновременно анализируется момент импульса тела L→{\displaystyle {\vec {L}}}, то начало O всегда выбирается одинаковым для L→{\displaystyle {\vec {L}}} и M→{\displaystyle {\vec {M}}}.

Если не оговорено иное, то «момент силы» — это момент силы относительно точки (O), а не некоей оси.

В случае нескольких приложенных сосредоточенных сил их моменты векторно суммируются:

M→=∑ir→i×F→i{\displaystyle {\vec {M}}=\sum _{i}\left},

где r→i{\displaystyle {\vec {r}}_{i}} — радиус-вектор точки приложения i{\displaystyle i}-й силы F→i{\displaystyle {\vec {F}}_{i}}. В случае силы, распределённой с плотностью dF→dV{\displaystyle d{\vec {F}}/dV},

M→=∫Vr→×dF→dVdV{\displaystyle {\vec {M}}=\int \limits _{V}\leftdV}.

Если dF→dV{\displaystyle d{\vec {F}}/dV} (Н/м3) — обобщённая функция, которая может содержать и дельтаобразные члены, то последней формулой охватываются и две предыдущие.

Момент силы относительно оси

Моментом силы относительно оси называется алгебраическое значение проекции момента M→{\displaystyle {\vec {M}}} на ось, то есть

M∥=M→⋅e→o{\displaystyle M_{\parallel }={\vec {M}}\cdot {\vec {e}}_{o}},

где e→o{\displaystyle {\vec {e}}_{o}} — единичный вектор вдоль оси, а начало отсчёта O выбрано на оси. Момент силы относительно оси может быть рассчитан как

M∥=±|r→⊥×F→⊥|{\displaystyle M_{\parallel }=\pm \left|{\vec {r}}_{\perp }\times {\vec {F}}_{\perp }\right|},

где через r→⊥{\displaystyle {\vec {r}}_{\perp }} и F→⊥{\displaystyle {\vec {F}}_{\perp }} обозначены составляющие радиус-вектора и силы в плоскости, перпендикулярной оси.

В отличие от момента силы M→{\displaystyle {\vec {M}}}, величина момента силы относительно оси M∥{\displaystyle M_{\parallel }} не претерпевает изменения при сдвиге точки O вдоль оси.

Для краткости, символ параллельности и знак могут опускаться, а M∥{\displaystyle M_{\parallel }} (как и M→{\displaystyle {\vec {M}}}) именоваться «моментом силы».

Единицы измерения

Момент силы имеет размерность «сила, умноженная на расстояние» и единицу измерения ньютон-метр (джоуль) в системе СИ. 1 Н·м — это момент, который производит сила 1 Н на рычаг длиной 1 м, приложенная к концу рычага и направленная перпендикулярно ему.

Размерность M→{\displaystyle {\vec {M}}} совпадает с размерностями энергии и механической работы.

Связь с другими величинами

С моментом импульса

Зависимости между силой F, моментом силы τ (M), импульсом p и моментом импульса L в системе, которая была ограничена только в одной плоскости (силы и моменты, обусловленные тяжестью и трением, не учитываются).

Момент силы — производная момента импульса L→=r→×p→{\displaystyle {\vec {L}}={\vec {r}}\times {\vec {p}}} относительно точки O по времени:

M→=dL→dt{\displaystyle {\vec {M}}={\frac {d{\vec {L}}}{dt}}},

Аналогичную формулу можно записать для моментов относительно оси:

M∥=dL∥dt{\displaystyle M_{\parallel }={\frac {dL_{\parallel }}{dt}}}.

Если момент силы M→{\displaystyle {\vec {M}}} или M∥{\displaystyle M_{\parallel }} равен нулю, момент импульса относительно соответствующей точки или оси сохраняется.

С мощностью

Если сила совершает действие на каком-либо расстоянии, то она совершает механическую работу и развивает мощность F→⋅v→{\displaystyle {\vec {F}}\cdot {\vec {v}}} (где v→{\displaystyle {\vec {v}}} — скорость материальной точки). Так же и в случае момента силы: если он совершает действие через «угловое расстояние», развивается мощность

P=M→⋅ω→{\displaystyle P={\vec {M}}\cdot {\vec {\omega }}}.

В системе СИ мощность P{\displaystyle P} измеряется в ваттах, угловая скорость ω→{\displaystyle {\vec {\omega }}} — в радианах в секунду.

С механической работой

Если под действием момента силы M→{\displaystyle {\vec {M}}} происходит поворот тела на угол dφ{\displaystyle d\varphi }, то совершается механическая работа

dA=|M→|dφ{\displaystyle dA=\left|{\vec {M}}\right|d\varphi }.

Для поворота, скажем, рычага вокруг фиксированной оси на угол φ2−φ1{\displaystyle \varphi _{2}-\varphi _{1}} получим

A=∫φ1φ2|M→|dφ=|M→|(φ2−φ1)=|M→|∫t1t2ω(t)dt{\displaystyle A=\int _{\varphi _{1}}^{\varphi _{2}}\left|{\vec {M}}\right|d\varphi =\left|{\vec {M}}\right|(\varphi _{2}-\varphi _{1})=\left|{\vec {M}}\right|\int _{t_{1}}^{t_{2}}\omega (t)dt}.

В системе СИ работа A{\displaystyle A} измеряется в джоулях, угол — в радианах.

Размерность работы (и энергии) совпадает с размерностью момента силы («ньютон на метр» и джоуль — это одни и те же единицы). Момент силы 1 Н·м, при повороте рычага или вала на 1 радиан совершает работу в 1 Дж, а при повороте на один оборот совершает механическую работу и сообщает энергию 2π{\displaystyle 2\pi } джоуля.

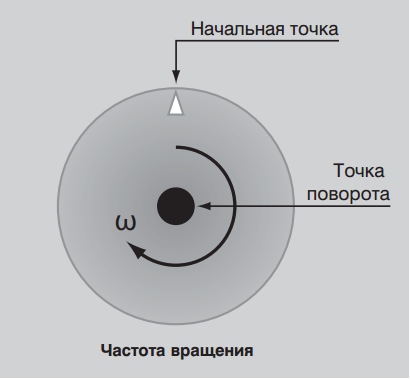
Момент вращения относительно оси

Эту физическую величину также называют моментом импульса. Слово «момент» означает, что при определении соответствующей характеристики учитывается положение оси вращения. Так, момент импульса частицы массой m, которая вращается со скоростью v вокруг оси O и находится от последней на расстоянии r, описывается следующей формулой:

Знак «¯» указывает на векторный характер соответствующей величины. Направление вектора момента вращения L¯ определяется по правилу правой руки (четыре пальца направлены от конца вектора r¯ к концу p¯, и отставленный большой палец показывает, куда будет направлен L¯). Направления всех названных векторов можно посмотреть на главном фото статьи.

При решении практических задач пользуются формулой для момента импульса в форме скалярной. Кроме того, линейную скорость заменяют угловой. В этом случае формула для L будет выглядеть так:

Величина m*r2 обозначается буквой I и называется моментом инерции. Она характеризует инерционные свойства системы вращения. В общем виде выражение для L записывается так:

Эта формула справедлива не только для вращающейся частицы массой m, но и для любого тела произвольной формы, которое совершает круговые перемещения относительно некоторой оси.

Качение деревянного диска

Имеется диск из дерева, его радиус r равен 0,5 метра. Этот диск начинают катить по деревянной поверхности. Необходимо рассчитать, какое расстояние способен он преодолеть, если начальная скорость вращения его ω составляла 5 рад/с.

Кинетическая энергия вращающегося тела равна:

Здесь I — момент инерции. Сила трения качения будет приводить к замедлению движения диска. Работу, совершаемую ей, можно вычислить по следующей формуле:

Здесь θ — угол в радианах, на который сможет повернуться диск в процессе своего движения. Тело будет катиться до тех пор, пока вся его кинетическая энергия не расходуется на работу трения, то есть можно приравнять выписанные формулы:

Момент инерции диска I равен m*r2/2. Чтобы вычислить момент M силы трения F, следует заметить, что она действует вдоль края диска в точке его соприкосновения с деревянной поверхностью, то есть M = r*F. В свою очередь F = f*mg/r (сила реакции опоры N равна весу диска mg). Подставляя все эти формулы в последнее равенство, получим:

Поскольку пройденное диском расстояние L связано с углом θ выражением L=r*θ, то получаем конечное равенство:

Значение f можно посмотреть в таблице для коэффициентов трения качения. Для пары дерево-дерево он равен 1,5*10-3 м. Подставляем все величины, получаем:

Для подтверждения правильности полученной конечной формулы можно проверить, что получаются единицы измерения длины.

Общие сведения

В физике момент силы можно понимать как «вращающая сила». В Международной системе единиц (СИ) единицей измерения момента силы является ньютон-метр. Момент силы иногда называют моментом пары сил, это понятие возникло в трудах Архимеда над рычагами. В простейшем случае, если сила приложена к рычагу перпендикулярно ему, момент силы определяется как произведение величины этой силы на расстояние до оси вращения рычага. Например, сила в 3 ньютона, приложенная к рычагу на расстоянии 2 метра от его оси вращения, создаёт такой же момент, что и сила в 1 ньютон, приложенная к рычагу на расстоянии 6 метров от оси вращения. Более точно момент силы частицы определяется как векторное произведение:

M→=r→×F→,{\displaystyle {\vec {M}}=\left,}

где F→{\displaystyle {\vec {F}}} — сила, действующая на частицу, а r→{\displaystyle {\vec {r}}} — радиус-вектор частицы.

О чем пойдет речь?

Многие люди наверняка обращали внимание, что если воздействовать с какой-либо силой на предмет, закрепленный в некоторой точке, то он начинает вращаться. Ярким примером может служить дверь в дом или в комнату

Если ее взять за ручку и толкнуть (приложить силу), то она начнет открываться (поворачиваться на петлях). Этот процесс представляет собой проявление в быту действия физической величины, которая получила название момента силы.

Из описанного примера с дверью следует, что рассматриваемая величина указывает на способность силы совершать вращение, что является ее физическим смыслом. Также эту величину называют моментом кручения.

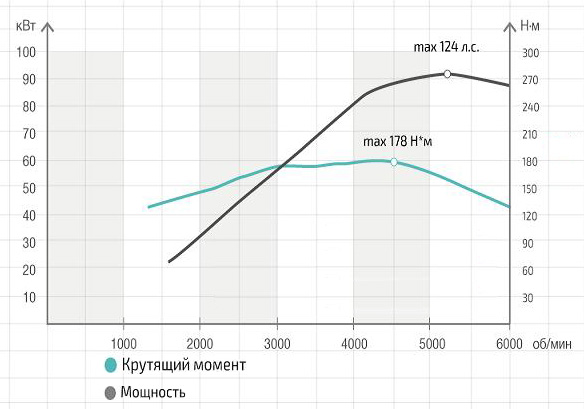
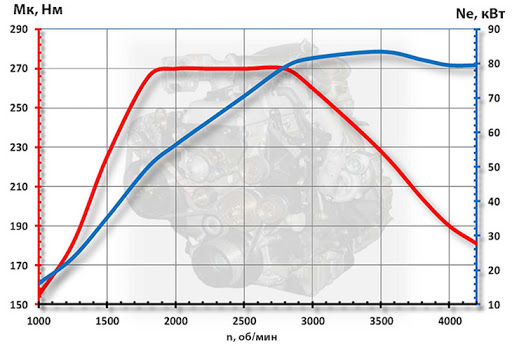
Что такое крутящий момент двигателя автомобиля простыми словами

Крутящий момент и мощность двигателей ВАЗ. Как видно из графиков, максимальная мощность достигается только на максимальных оборотах, тогда как пик крутящего момента находится между 3000 и 4500 оборотов.

Чтобы ответить на этот вопрос простыми словами нужно сначала выяснить, что подразумевается под терминами «мощность», «крутящий момент», а также число оборотов. С первой из этих характеристик дело обстоит несколько проще, поскольку всем тем, кто хорошо учился в средней школе, известно, что мощность — это работа, производимая в единицу времени.

Двигатель внутреннего сгорания, потребляя топливо, преобразовывает тепловую энергию его сгорания в кинетическую, совершая при этом работу. Она заключается во вращении коленчатого вала, и этот показатель измеряется в количестве оборотов в минуту. Соответственно, от частоты, с которой в цилиндрах ДВС происходит сгорание топливной смеси, напрямую зависит и работа, которую производит двигатель, и его мощность. Зависимость эта — прямо пропорциональная.

Что же касается крутящего момента, то с ним отнюдь не все так очевидно, как с мощностью и количеством оборотов. Он является, по сути дела, величиной, производной от них и представляет собой произведение силы на плечо рычага. Поскольку сила (в данном случае та, которая возникает при сгорании топлива и воздействует на поршень) измеряется в физике в ньютонах, а длина (в данном случае — длина плеча кривошипа коленчатого вала) — в метрах, то единицей измерения крутящего момента, является Нм.

Таким образом, получается, что крутящий момент представляет собой усилие, которое развивает двигатель. Именно его значение определяет силу тяги, обеспечивающую разгон автомобиля и его движение. Следовательно, чем больше крутящий момент, тем автомобиль «резвее», что есть тем лучше его динамика. Поскольку сила, воздействующая на поршень при сгорании топлива, растет с увеличением рабочего объема двигателя, то чем он больше, тем выше крутящий момент.

Следует заметить, что в характеристиках двигателей внутреннего сгорания всегда указывается максимальная мощность, которую они способны развить. Крутящий момент определяет, как быстро она достигается, и поэтому он указывается для конкретного числа оборотов. Иными словами, он определяет, как быстро силовой агрегат «выбирает» тот потенциал мощности, который в нем заложен конструкторами. Именно поэтому, к примеру, при достаточно спокойной езде на невысоких оборотах (до 2500 об/мин) для быстрого ускорения самым предпочтительным двигателем является тот, который имеет максимальный крутящий момент именно на них.

Крутящий момент и лошадиная сила

Автолюбители нередко дискутируют друг с другом: чей двигатель мощнее. Но иногда и не представляют при этом, из чего складывается данный параметр. Общепринятый термин «лошадиная сила» был введён изобретателем Джеймсом Уаттом в XVIII веке.  Он придумал его, наблюдая за лошадью, которая была запряжена в поднимающий уголь из шахты механизм. Он рассчитал, что одна лошадь за минуту может поднять 150 кг угля на высоту 30-ти метров. Одна лошадиная сила эквивалентна 735,5 Ватт, или 1 кВт равен 1,36 л.с.

В первую очередь, мощность любого мотора оценивают в лошадиных силах, и лишь потом вспоминают о крутящем моменте. Но эта тяговая характеристика тоже даёт представление о конкретных тягово-динамических возможностях автомобиля. Крутящий момент является показателем работы силового агрегата, а мощность – основным параметром выполнения этой работы. Эти показатели тесно связаны друг с другом. Чем больше производится двигателем лошадиных сил, тем больше и потенциал крутящего момента. Реализуется этот потенциал в реальных условиях через трансмиссию и полуоси машины. Соединение этих элементов вместе и определяет, как именно мощность может переходить в крутящий момент.

Простейший пример – сравнение трактора с гоночной машиной. У гоночного болида лошадиных сил много, но крутящий момент требуется для увеличения скорости через редуктор. Чтобы такая машина двигалась вперёд, надо совсем немного работы, потому что основная часть мощности используется для развития скорости.

Что касается трактора, то у него может быть мотор с таким же рабочим объёмом, который вырабатывает столько же лошадиных сил. Но мощность в этом случае используется не для развития скорости, а для выработки тяги (См. тяговый класс). Для этого она пропускается через многоступенчатую трансмиссию. Поэтому трактор не развивает высоких скоростей, зато он может буксировать большие грузы, пахать и культивировать землю, и т.д.

В двигателях внутреннего сгорания сила передаётся от газов сгорающего топлива поршню, от поршня – передаётся на кривошипный механизм, и далее на коленчатый вал. А коленвал, через трансмиссию и приводы, раскручивает колёса.

Естественно, крутящий момент двигателя не постоянен. Он сильней, когда на плечо действует бо́льшая сила, и слабей – когда сила слабнет или перестаёт действовать. То есть, когда водитель давит на педаль газа, то сила, воздействующая на плечо, повышается, и, соответственно увеличивается крутящий момент двигателя.

Мощность обеспечивает преодоление всевозможных сил, которые мешают двигаться автомобилю. Это и сила трения в двигателе, трансмиссии и в приводах автомобиля, и аэродинамические силы, и силы качения колёс и т.д. Чем больше мощность, тем большее сопротивление сил машина сможет преодолеть и развить большую скорость. Однако мощность – сила не постоянная, а зависящая от оборотов мотора. На холостом ходу мощность одна, а на максимальных оборотах – совершенно другая. Многими автопроизводителями указывается, при каких оборотах достигается максимально возможная мощность автомобиля.

Необходимо учитывать, что максимальная мощность не развивается сразу. Автомобиль стартует с места практически при минимальных оборотах (немного выше холостого хода), и для того, чтобы отмобилизировать полную мощность, требуется время. Тут и вступает в дело крутящий момент двигателя. Именно от него и будет зависеть, за какой отрезок времени автомашина достигнет своей максимальной мощности – то есть, динамика её разгона.

Зачастую водитель сталкивается с такими ситуациями, когда требуется придать автомобилю значительное ускорение для выполнения необходимого маневра. Прижимая педаль акселератора в пол, он чувствует, что автомобиль ускоряется слабо. Для быстрого ускорения нужен мощный крутящий момент. Именно он и характеризует приёмистость автомобиля.

Основную силу в двигателе внутреннего сгорания вырабатывает камера сгорания, в которой воспламеняется топливно-воздушная смесь. Она приводит в действие кривошипно-шатунный механизм, а через него – коленчатый вал. Рычагом является длина кривошипа, то есть, если длина будет больше, то и крутящий момент тоже увеличится.

Однако увеличивать кривошипный рычаг до бесконечности невозможно. Ведь тогда придётся увеличивать рабочий ход поршня, а вместе с ним и размеры двигателя. При этом уменьшатся и обороты двигателя. Двигатели с большим рычагом кривошипного механизма можно применить только лишь в крупномерных плавательных средствах. А в легковых автомашинах с небольшими размерами коленчатого вала не поэкспериментируешь.

Мощность вращающихся объектов

Для расчета подобной системы применяют формулу:

N = M * w = (2π * M* n)/60,

где:

• M – момент силы;
• w – угловая скорость, характеризующая вращение;
• n – количество оборотов, которое совершает двигатель или другое устройство за 60 секунд.

Приведенные сведения используют с учетом целевого назначения и реальных условий. Так, в термодинамике необходимо помнить о зависимости эффективности системы от температуры окружающей среды. Тепловые потери нагревателя оценивают по соответствующей мощности на единицу площади поверхности. Аналогичным образом поступают при решении механических задач для расчета тяги, КПД, иных рабочих параметров. Как правило, приходится специальным коэффициентом компенсировать трение.

В электрических цепях ток ограничивает сопротивление проводника. Для небольших расстояний при малой мощности тщательные расчеты не нужны. Однако проект магистральной трассы обязательно содержит соответствующие вычисления. На основе полученных результатов делают выводы о среднегодовых экономических показателях. Следует помнить о необходимости учета искажений, которые добавляют при работе с переменным напряжением реактивные нагрузки.

Физический смысл величины M¯

В физике и механике вращения величина M¯ определяет способность силы или суммы сил совершать вращение. Поскольку в математическом определении величины M¯ стоит не только сила, но и радиус-вектор ее приложения, то именно последний во многом определяет отмеченную вращательную способность. Чтобы понятнее было, о какой способности идет речь, приведем несколько примеров:

Каждый человек, хотя бы один раз в жизни пытался открыть дверь, взявшись не за ручку, а толкнув ее недалеко от петель. В последнем случае приходится прилагать значительное усилие, чтобы добиться желаемого результата. Чтобы открутить гайку с болта, используют специальные гаечные ключи. Чем длиннее ключ, тем легче открутить гайку

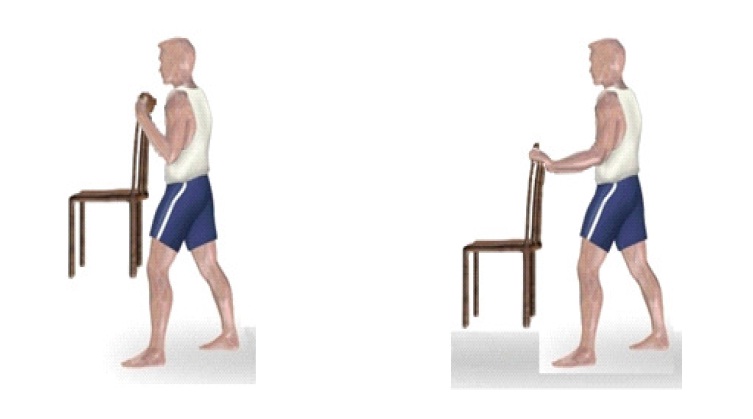
Чтобы ощутить важность рычага силы, предлагаем читателям проделать следующий эксперимент: взять стул и попытаться удержать его одной рукой на весу, в одном случае руку прислонить к телу, в другом — выполнить задачу на прямой руке. Последнее для многих окажется непосильной задачей, хотя вес стула остался тем же самым

Пусковой ток и его кратность

Чтобы тронуть с места (пустить) двигатель, нужен громадный пусковой ток (Iп). Громадный – по сравнению с номинальным (рабочим) током Iн на установившейся скорости. В статьях обычно указывают, что пусковой ток превышает рабочий в 5-8 раз. Это число называется “Кратность пускового тока” и обозначается как коэффициент Кп = Iп / Iн.

Пусковой ток – это ток, который потребляет электродвигатель во время пуска. Узнать пусковой ток можно, зная номинальный ток и коэффициент Кп:

Iп = Кп · Iн

Номинальный ток всегда указан на шильдике двигателя:

Номинальный ток двигателя для разных напряжений и схем включения

Кп – рабочий параметр, который указан в характеристиках двигателя, но на корпусе двигателя он никогда не указывается.

Кратность пускового тока . На шильдике его обычно нет, а в документации и на сайтах производителей он присутствует:

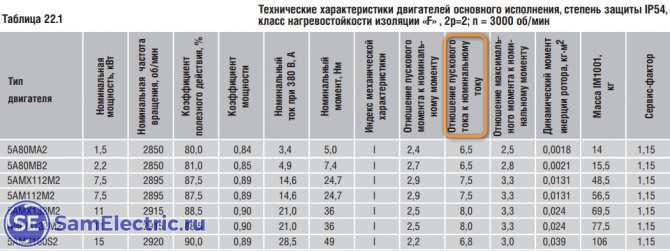
Параметры двигателей. Кратность пускового тока

Судя по каталогам (их можно будет скачать в конце статьи, как обычно у меня), пусковой ток превышает номинальный в пределах от 3,5 до 8,5 раз. Кратность пускового тока зависит прежде всего от мощности двигателя и от количества пар полюсов. Чем меньше мощность, тем меньше пусковой ток. А чем меньше пар полюсов (больше номинальные обороты) – тем больше пусковой ток.

Так происходит потому, что потребляемый ток и момент инерции при пуске зависит от конструкции двигателя и способа намотки. Мало полюсов – низкое сопротивление обмоток. Низкое сопротивление – большой ток. Кроме того, высокооборотистым движкам для полной раскрутки требуется больше времени, а это опять же тяжелый пуск.

Если объяснить более научным языком, то дело происходит так. Когда двигатель стоит, его степень скольжения S = 1. При раскручивании (или, как любят говорить спецы, разворачивании) S стремится к нулю, но никогда его не достигает – на то двигатель и называют асинхронным, ведь вращение ротора никогда не догонит вращение поля статора из-за потерь. Одновременно сердечник ротора насыщается магнитным полем, увеличивается ЭДС самоиндукции и индукционное сопротивление. А значит, уменьшается ток.

На самом деле не так всё просто, начинаем копать глубже.

Связь с другими величинами

С моментом импульса

Зависимости между силой F, моментом силы τ (M), импульсом p и моментом импульса L в системе, которая была ограничена только в одной плоскости (силы и моменты, обусловленные тяжестью и трением, не учитываются).

Момент силы — производная момента импульса L→=r→×p→{\displaystyle {\vec {L}}={\vec {r}}\times {\vec {p}}} относительно точки O по времени:

M→=dL→dt{\displaystyle {\vec {M}}={\frac {d{\vec {L}}}{dt}}},

Аналогичную формулу можно записать для моментов относительно оси:

M∥=dL∥dt{\displaystyle M_{\parallel }={\frac {dL_{\parallel }}{dt}}}.

Если момент силы M→{\displaystyle {\vec {M}}} или M∥{\displaystyle M_{\parallel }} равен нулю, момент импульса относительно соответствующей точки или оси сохраняется.

С мощностью

Если сила совершает действие на каком-либо расстоянии, то она совершает механическую работу и развивает мощность F→⋅v→{\displaystyle {\vec {F}}\cdot {\vec {v}}} (где v→{\displaystyle {\vec {v}}} — скорость материальной точки). Так же и в случае момента силы: если он совершает действие через «угловое расстояние», развивается мощность

P=M→⋅ω→{\displaystyle P={\vec {M}}\cdot {\vec {\omega }}}.

В системе СИ мощность P{\displaystyle P} измеряется в ваттах, угловая скорость ω→{\displaystyle {\vec {\omega }}} — в радианах в секунду.

С механической работой

Если под действием момента силы M→{\displaystyle {\vec {M}}} происходит поворот тела на угол dφ{\displaystyle d\varphi }, то совершается механическая работа

dA=|M→|dφ{\displaystyle dA=\left|{\vec {M}}\right|d\varphi }.

Для поворота, скажем, рычага вокруг фиксированной оси на угол φ2−φ1{\displaystyle \varphi _{2}-\varphi _{1}} получим

A=∫φ1φ2|M→|dφ=|M→|(φ2−φ1)=|M→|∫t1t2ω(t)dt{\displaystyle A=\int _{\varphi _{1}}^{\varphi _{2}}\left|{\vec {M}}\right|d\varphi =\left|{\vec {M}}\right|(\varphi _{2}-\varphi _{1})=\left|{\vec {M}}\right|\int _{t_{1}}^{t_{2}}\omega (t)dt}.

В системе СИ работа A{\displaystyle A} измеряется в джоулях, угол — в радианах.

Размерность работы (и энергии) совпадает с размерностью момента силы («ньютон на метр» и джоуль — это одни и те же единицы). Момент силы 1 Н·м, при повороте рычага или вала на 1 радиан совершает работу в 1 Дж, а при повороте на один оборот совершает механическую работу и сообщает энергию 2π{\displaystyle 2\pi } джоуля.