Коэффициент жесткости пружины

Жесткость пружины. Как рассчитать.

Измерение параметров жесткости пружин разных типов

При производстве на предприятии и для применения необходимо определить способность пружины выдерживать определенные типы нагрузок. Для этого высчитывается т.н. коэффициент Гука – обозначение жесткости пружины, от которого зависит её надёжность. На этот параметр влияет материал, выбранный для изготовления. Это может быть сталь, легированная кремнием, ванадием, марганцем, другими добавками. Также применяются нержавейка, бериллиевая и кремнемарганцевая бронза, сплавы на основе никеля и титана. Если деталь выпускается для применения при высоких нагрузках, экстремальных температурах, используются специальные марки легированной стали. Нижегородская метизная корпорация имеет возможность производить пружины под заказ, создавая изделия с заданными характеристиками.

Что такое жесткость?

Говоря о практике, а не физических терминах, это сила, приложив которую, можно сжать пружину. Если вы знаете прилагаемое усилие, можно определить, какой будет деформация, и наоборот. Это существенно облегчает вычисления.

Коэффициент высчитывается для пружин кручения, растяжения, изгиба, сжатия – всех наиболее популярных в промышленности разновидностей этого изделия. Также следует отметить два основных типа:

• С линейной (постоянной) жесткостью;
• С прогрессивной (зависящей от положения витков) жесткостью.

Часто производитель наносит на готовую продукцию пометку краской. Если такого обозначения нет, применяется формула определения жесткости пружины через массу и длину, упрощающая задачу. Она изначально разрабатывалась для пружин растяжения, была получена методом измерения соответствия массы грузы с изменениями геометрии.

Также данный параметр может быть прогрессирующим – растущим — или регрессирующим – убывающим. Во втором случае параметр «жесткости» принято называть «мягкостью». В отдельных механизмах, например, в автомобилестроении, этот параметр особенно актуален.

Какие вводные данные требуются?

При расчёте важно знать следующую информацию:

• Из какого материала выполнено изделие;
• Точный диаметр витков – Dw ;
• Общий диаметр самой пружины – Dm ;
• Количество витков – Na .

Таким образом, к коэффициенту жесткости пружинного механизма может применяться формула:

k=G*(Dw)^4/8 * Na * (Dm)^3

Переменная G

означает модуль сдвига. Это значение можно найти в таблицах для разных материалов. К примеру, у пружинной сталиG=78,5 ГПа .

Далее разберемся, как определить жесткость пружины по формуле:

k=F/L.

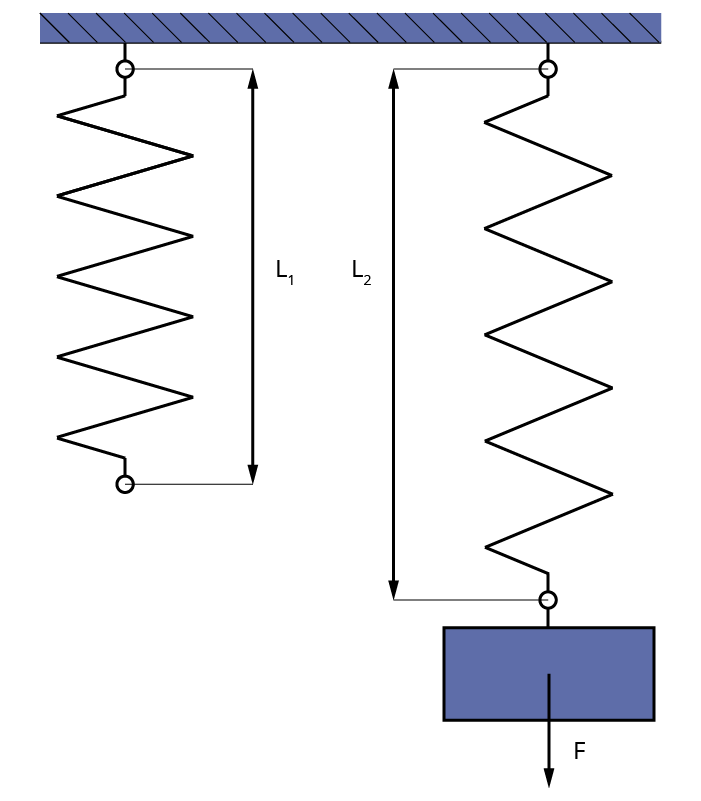
Длина L

бывает двух типов:

• L1 – измеренная в вертикальном положении без груза;
• L2 – полученная при подвешивании груза с точно известной массой.

Например, 100

-граммовая гиря, закреплённая в нижней части, воздействует с силойF , равной1 Н . Получаем разницу между двумя показателями длины:

L = L2 – L1

При этом следует уточнить, что степень жесткости не определяет распрямление в исходное состояние. На него воздействуют сразу несколько факторов.

Насколько важен показатель, и на что он влияет?

Характеристики пружины важны не только для соответствия ГОСТам и проведения сертификации. Они влияют на сроки эксплуатации изделий, в которых используются, а это огромное количество приборов, деталей, механизмов, от мебели, до различных транспортных средств.

Поэтому данная величина напрямую влияет на надёжность готовых изделий, оборудования, техники, в которых используются элементы, содержащие пружины.

Часто люди интересуются, как рассчитать жесткость пружины цилиндрической винтовой. Для таких случаев учитывается не только модуль сдвига, но и параметр Rs

– напряжение, допускаемое при кручении. Здесь в расчёт берётся тип материала, его физические свойства, механические характеристики.

Следующий вопрос – в чем измеряется коэффициент жесткости пружины при расчётах. Традиционно в системе измерений, принятой в нашей стране принято записывать значение в Н/м

– ньютонах на один метр. Также это значение в качестве альтернативного варианта может записываться в килограммах на квадратный сантиметр, дин/см, граммах на квадратный сантиметр (расчёты в системе СГС).

Физика

Закон Гука

Пока пружины не растянуты или сжимаются сверх предела упругости , большинство пружин подчиняются закону Гука, который гласит, что сила, с которой пружина отталкивает, линейно пропорциональна расстоянию от ее равновесной длины:

Fзнак равно-kИкс, {\ Displaystyle F = -kx, \}

где

x — вектор смещения — расстояние и направление, в котором пружина деформируется относительно ее равновесной длины.

F — результирующий вектор силы — величина и направление возвращающей силы, оказываемой пружиной.

K представляет собой скорость , пружины или силовая константа пружины, константа , которая зависит от материала и конструкции весной в. Отрицательный знак указывает на то, что сила, которую оказывает пружина, находится в направлении, противоположном ее смещению.

Винтовые пружины и другие обычные пружины обычно подчиняются закону Гука. Есть полезные пружины, которые этого не делают: пружины, основанные на изгибе балки, могут, например, создавать силы, которые нелинейно изменяются с перемещением.

Конические пружины , изготовленные с постоянным шагом (толщиной проволоки), имеют переменную скорость. Однако можно сделать коническую пружину постоянной жесткостью, создав пружину с переменным шагом. Больший шаг катушек большего диаметра и меньший шаг катушек меньшего диаметра заставляет пружину сжиматься или растягиваться с одинаковой скоростью при деформации.

Простые гармонические колебания

Поскольку сила равна массе m , умноженной на ускорение a , уравнение силы для пружины, подчиняющейся закону Гука, выглядит так:

Fзнак равнома⇒-kИксзнак равнома.{\ Displaystyle F = ma \ quad \ Rightarrow \ quad -kx = ma. \,}

Смещение x как функция времени. Время, которое проходит между пиками, называется периодом .

Масса пружины мала по сравнению с массой присоединенной массы и не учитывается. Поскольку ускорение — это просто вторая производная от x по времени,

-kИксзнак равномd2Иксdт2.{\ displaystyle -kx = m {\ frac {d ^ {2} x} {dt ^ {2}}}. \,}

Это линейное дифференциальное уравнение второго порядка для смещения как функции времени. Перестановка:
Икс{\ displaystyle x}

d2Иксdт2+kмИксзнак равно,{\ displaystyle {\ frac {d ^ {2} x} {dt ^ {2}}} + {\ frac {k} {m}} x = 0, \,}

решение которого является суммой синуса и косинуса :

Икс(т)знак равноАгрех⁡(тkм)+Bпотому что⁡(тkм).{\ displaystyle x (t) = A \ sin \ left (t {\ sqrt {\ frac {k} {m}}} \ right) + B \ cos \ left (t {\ sqrt {\ frac {k} { m}}} \ right). \,}

А{\ displaystyle A}и являются произвольными константами, которые можно найти, рассматривая начальное смещение и скорость массы. График этой функции с (нулевое начальное положение с некоторой положительной начальной скоростью) отображается на изображении справа.
B{\ displaystyle B}Bзнак равно{\ displaystyle B = 0}

Коэффициент жесткости цилиндрической пружины

На практике и в физике довольно большое распространение получили именно цилиндрические пружины. Их ключевыми особенностями можно назвать следующие моменты:

1. При создании указывается центральная ось, вдоль которой и действует большинство различных сил.
2. При производстве рассматриваемого изделия применяется проволока определенного диаметра. Она изготавливается из специального сплава или обычных металлов. Не стоит забывать о том, что материал должен обладать повышенной упругостью.
3. Проволока накручивается витками вдоль оси. При этом стоит учитывать, что они могут быть одного или разного диаметра. Довольно большое распространение получил вариант исполнения цилиндрического типа, но большей устойчивостью характеризуется цилиндрический вариант исполнения, в сжатом состоянии деталь обладает небольшой толщиной.
4. Основными параметрами можно назвать больший, средний и малый диаметр витков, диаметр проволоки, шаг расположения отдельных колец.

Не стоит забывать о том, что выделяют два типа деталей: сжатия и растяжения. Их коэффициент жесткости определяется по одной и той же формуле. Разница заключается в следующем:

1. Вариант исполнения, рассчитанный на сжатие, характеризуется дальним расположением витков. За счет расстояние между ними есть возможность сжатия.
2. Модель, рассчитанная на растяжение, имеет кольца, расположенные практически вплотную. Подобная форма определяет то, что при максимальная сила упругости достигается при минимальном растяжении.
3. Также есть вариант исполнения, который рассчитан на кручение и изгиб. Подобная деталь рассчитывается по определенным формулам.

Расчет коэффициента цилиндрической пружины может проводится при использовании ранее указанной формулы. Она определяет то, что показатель зависит от следующих параметров:

1. Наружного радиуса колец. Как ранее было отмечено, при изготовлении детали применяется ось, вокруг которой проводится накручивание колец. При этом не стоит забывать о том, что выделяют также средний и внутренний диаметр. Подобный показатель указывается в технической документации и на чертежах.
2. Количества создаваемых витков. Этот параметр во многом определяет длину изделия в свободном состоянии. Кроме этого, количество колец определяет коэффициент жесткость и многие другие параметры.
3. Радиуса применяемой проволоки. В качестве исходного материала применяется именно проволока, которая изготавливается из различных сплавов. Во многом ее свойства оказывают влияние на качества рассматриваемого изделия.
4. Модуля сдвига, который зависит от типа применяемого материала.

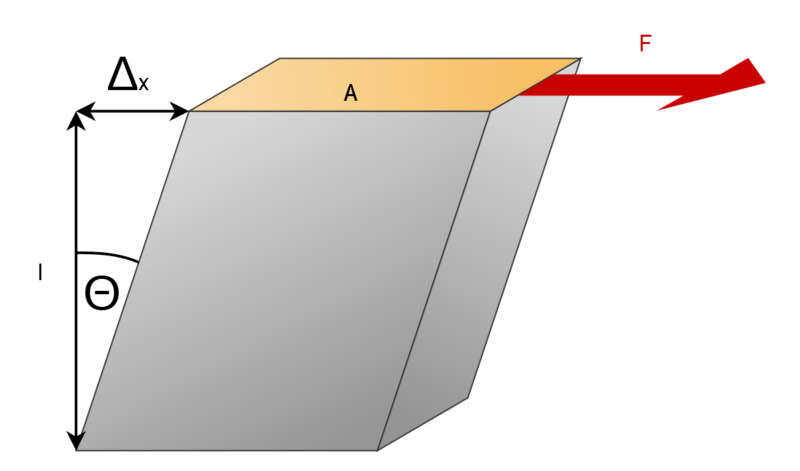
Коэффициент жесткости считается одним из наиболее важных параметров, который учитывается при проведении самых различных расчетов.

1.12. Сила упругости. Закон Гука window.top.document.title = «1.12. Сила упругости. Закон Гука»;

При деформации тела возникает сила, которая стремится восстановить прежние размеры и форму тела. Эта сила возникает вследствие электромагнитного взаимодействия между атомами и молекулами вещества. Ее называют силой упругости.

Простейшим видом деформации являются деформации растяжения и сжатия (рис. 1.12.1).

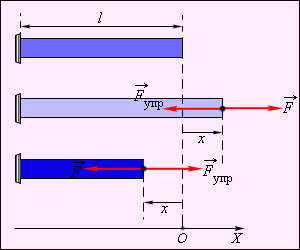Рисунок 1.12.1.Деформация растяжения (x > 0) и сжатия (x < 0). Внешняя сила

При малых деформациях (|x| << l) сила упругости пропорциональна деформации тела и направлена в сторону, противоположную направлению перемещения частиц тела при деформации:

Это соотношение выражает экспериментально установленный закон Гука. Коэффициент k называется жесткостью тела. В системе СИ жесткость измеряется в ньютонах на метр (Н/м). Коэффициент жесткости зависит от формы и размеров тела, а также от материала. В физике закон Гука для деформации растяжения или сжатия принято записывать в другой форме. Отношение ε = x / l называется относительной деформацией, а отношение σ = F / S = –F_упр / S, где S – площадь поперечного сечения деформированного тела, называется напряжением. Тогда закон Гука можно сформулировать так: относительная деформация ε пропорциональна напряжению σ:

Коэффициент E в этой формуле называется модулем Юнга. Модуль Юнга зависит только от свойств материала и не зависит от размеров и формы тела. Модуль Юнга различных материалов меняется в широких пределах. Для стали, например, E ≈ 2·1011 Н/м2, а для резины E ≈ 2·106 Н/м2, т. е. на пять порядков меньше.

Закон Гука может быть обобщен и на случай более сложных деформаций. Например, при деформации изгиба упругая сила пропорциональна прогибу стержня, концы которого лежат на двух опорах (рис. 1.12.2).

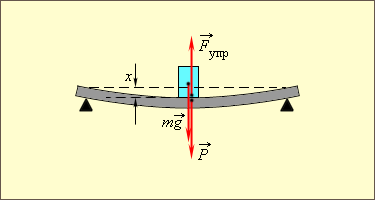Рисунок 1.12.2.Деформация изгиба.

Упругую силу действующую на тело со стороны опоры (или подвеса), называют силой реакции опоры. При соприкосновении тел сила реакции опоры направлена перпендикулярно поверхности соприкосновения. Поэтому ее часто называют силой нормального давления. Если тело лежит на горизонтальном неподвижном столе, сила реакции опоры направлена вертикально вверх и уравновешивает силу тяжести: Сила с которой тело действует на стол, называется .

В технике часто применяются спиралеобразные пружины (рис. 1.12.3). При растяжении или сжатии пружин возникают упругие силы, которые также подчиняются закону Гука. Коэффициент k называют жесткостью пружины. В пределах применимости закона Гука пружины способны сильно изменять свою длину. Поэтому их часто используют для измерения сил. Пружину, растяжение которой проградуировано в единицах силы, называют динамометром. Следует иметь в виду, что при растяжении или сжатии пружины в ее витках возникают сложные деформации кручения и изгиба.

Рисунок 1.12.3.Деформация растяжения пружины.

В отличие от пружин и некоторых эластичных материалов (резина) деформация растяжения или сжатия упругих стержней (или проволок) подчиняются линейному закону Гука в очень узких пределах. Для металлов относительная деформация ε = x / l не должна превышать 1 %. При больших деформациях возникают необратимые явления (текучесть) и разрушение материала.

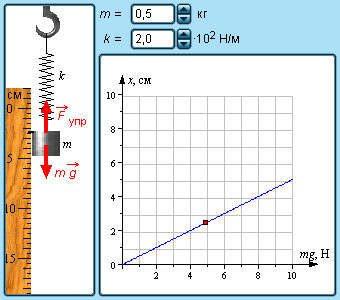Модель. Закон Гука

Видео

Из этого видео вы узнаете, как определить жесткость пружины.

Чем большей деформации подвергается тело, тем значительней в нем возникает сила упругости. Это значит, что деформация и сила упругости взаимосвязаны, и по изменению одной величины можно судить об изменении другой. Так, зная деформацию тела, можно вычислить возникающую в нем силу упругости. Или, зная силу упругости, определить степень деформации тела.

Если к пружине подвешивать разное количество гирек одинаковой массы, то чем больше их будет подвешено, тем сильнее пружина растянется, то есть деформируется. Чем больше растянута пружина, тем большая в ней возникает силы упругости. Причем опыт показывает, что каждая следующая подвешенная гирька увеличивает длину пружины на одну и туже величину.

Так, например, если исходная длина пружины была 5 см, а подвешивание на ней одной гирьки увеличило ее на 1 см (т. е. пружина стала длиной 6 см), то подвешивание двух гирек увеличит ее на 2 см (общая длина составит 7 см), а трех — на 3 см (длина пружины будет 8 см).

Еще до опыта известно, что вес и возникающая под его действием сила упругости находятся друг с другом в прямопропорциональной зависимости. Кратное увеличение веса во столько же раз увеличит силу упругости. Опыт же показывает, что деформация точно также зависит от веса: кратное увеличение веса во столько же раз увеличивает изменения в длине. Это значит, что, исключив вес, можно установить прямопропорциональную зависимость между силой упругости и деформацией.

Если обозначить удлинение пружины в результате ее растяжения как x или как ∆ l ( l ₁ – l , где l — начальная длина, l ₁ — длина растянутой пружины), то зависимость силы упругости от растяжения можно выразить такой формулой:

В формуле используется коэффициент k . Он показывает, в какой именно зависимости находятся сила упругости и удлинение. Ведь удлинение на каждый сантиметр может увеличивать силу упругости одной пружины на 0,5 Н, второй на 1 Н, а третьей на 2 Н. Для первой пружины формула будет выглядеть как F_упр = 0,5x, для второй — F_упр = x, для третьей — F_упр = 2x.

Коэффициент k называют жесткостью пружины. Чем жестче пружина, тем труднее ее растянуть, и тем большее значение будет иметь k. А чем больше k, тем больше будет сила упругости (F_упр) при равных удлинения (x) разных пружин.

Жесткость зависит от материала, из которого изготовлена пружина, ее формы и размеров.

Единицей измерения жесткости является Н/м (ньютон на метр). Жесткость показывает, сколько ньютонов (сколько сил) надо приложить к пружине, чтобы растянуть ее на 1 м. Или насколько метров растянется пружина, если приложить для ее растяжения силу в 1 Н. Например, к пружине приложили силу в 1 Н, и она растянулась на 1 см (0,01 м). Это значит, что ее жесткость равна 1 Н / 0,01 м = 100 Н/м.

Также, если обратить внимание на единицы измерения, то станет понятно, почему жесткость измеряется в Н/м. Сила упругости, как и любая сила, измеряется в ньютонах, а расстояние – в метрах

Чтобы уровнять по единицам измерения левую и правую части уравнения Fупр = kx, надо в правой части сократить метры (то есть поделить на них) и добавить ньютоны (то есть умножить на них).

Соотношение между силой упругости и деформацией упругого тела, описываемое формулой F_упр = kx, открыл английский ученый Роберт Гук в 1660 году, поэтому это соотношение носит его имя и называется законом Гука.

Упругой деформацией является такая, когда после прекращения действия сил, тело возвращается в свое исходное состояние. Бывают тела, которые почти нельзя подвергнуть упругой деформации, а у других она может быть достаточно большой. Например, поставив тяжелый предмет на кусок мягкой глины, вы измените его форму, и этот кусок сам уже не вернется в исходное состояние. Однако если вы растяните резиновый жгут, то после того, как отпустите его, он вернет свои исходные размеры. Следует помнить, что закон Гука применим только для упругих деформаций.

Формула F_упр = kx дает возможность по известным двум величинам вычислять третью. Так, зная приложенную силу и удлинение, можно узнать жесткость тела. Зная, жесткость и удлинение, найти силу упругости. А зная силу упругости и жесткость, вычислить изменение длины.

Влияние сопротивления на свободные колебания

Особенности детали определяют то, что при ее применении есть вероятность возникновения свободного колебательного движения. При этом имеет значение, какими особенностями обладает параллельно и последовательно соединенные пружины. Среди особенностей влияния сопротивления на свободное колебание отметим следующие моменты:

1. Проведенные тесты указывают на то, что параллельно соединенные пружины препятствуют возникновению свободного колебания. Это можно связать с существенным увеличением жесткости всей системы.
2. При последовательном расположении есть вероятность снижения сопротивления, так как расстояние между точкой крепления и телом существенно увеличивается.

Именно поэтому для существенного снижения колебательного вращения на момент эксплуатации системы рекомендуется использовать параллельный метод подключения.

Физические характеристики пружин

Цилиндрические пружины характеризуются рядом параметров, сочетание которых обуславливает их жесткость — способность сопротивляться деформации:

1. материал; пружины чаще всего изготавливают из стальной проволоки, причем сталь в них применялася особая, ее характеризует среднее или высокое содержание углерода, низкое содержание других примесей (низколегированный сплав) и особая термообработка (закалка), придающая материалу дополнительную упругость;
2. диаметр проволоки; чем он меньше, тем эластичнее пружина, но тем меньше ее способность запасать энергию; пружины сжатия изготавливают, как правило, из более толстой проволоки, чем пружины растяжения;
3. форма сечения проволоки; не всегда проволока, из которой намотана пружина, имеет круглое сечение; уплощенное сечение имеют пружины сжатия, чтобы при максимальном сокращении длины (виток «садится» на соседний виток) конструкция была более устойчивой;
4. длина и диаметр пружины; длину пружины следует отличать от длины проволоки, из которой она намотана; эти два параметра согласуются через количество витков и диаметр пружины, который, в свою очередь, не следует путать с диаметром проволоки.

Задай вопрос специалистам и получи ответ уже через 15 минут!

Существуют и другие физические характеристики, влияющие на работоспособность пружин. Например, при повышении температуры металл становится менее упругим, а при существенном ее понижении может стать хрупким. При интенсивной эксплуатации пружина со временем теряет часть упругости по причине постепенного разрушения связей между атомами кристаллической решетки.

Применение цилиндрических пружин

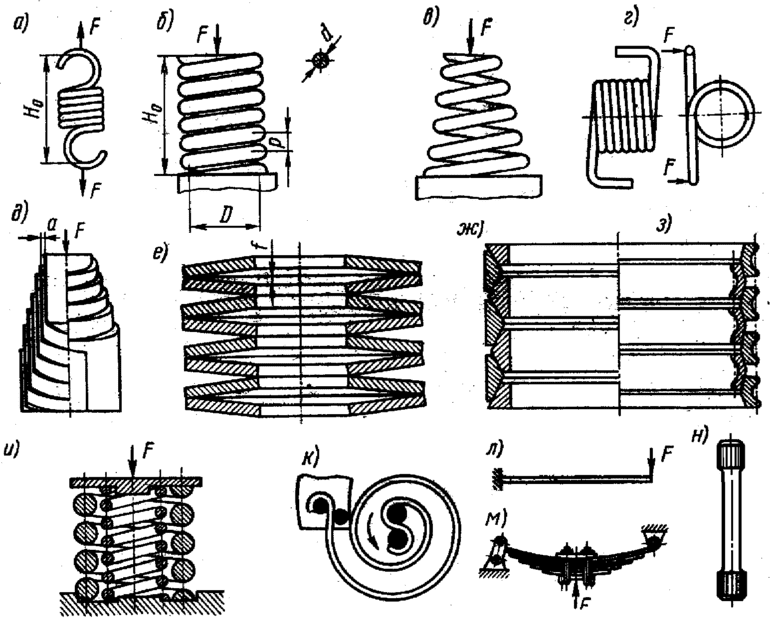
На производстве наиболее востребованы цилиндрические пружины, так как они обладают уникальными особенностями. При создании системы отмечается центральная ось, вдоль которой действуют разные силы. В процессе изготовления подобных изделий используется проволока соответствующего диаметра.

Для её изготовления понадобится специальный сплав либо обычные металлы. Сам материал должен обладать высокой упругостью. Проволока может иметь витки одного диаметра либо разных радиусов. Большим спросом пользуются цилиндрическая пружина, которая в сжатом состоянии обладает незначительной толщиной.

Главными параметрами изделия считаются:

• малый, средний и большой диаметр витков и самой проволоки;
• шаг размещения отдельный колец.

В задачах по физике вычисляется k для двух состояний: растяжение и сжатие. В любом случае используется одна формула для определения величины. Разница понятий:

Исполнение, рассчитанное на сжатие, характеризуется дальним размещением витков. Расстояние, образуемое между ними, появляется возможность на сжатие.
Модель, связанная с растяжением, имеет кольца, расположенные плотно между собой. Такая форма определяет то, что при максимальной силе растяжение минимальное.

Отдельно рассматриваются варианты на изгиб и кручение. Такие детали рассчитываются по специальным формулам. Для разных соединений характерны определённые особенности. Чтобы провести определения растяжения, учитывается момент теста.

Показатель зависит от характеристик проволоки, оказываемой силы либо массы тела. Для всех систем используются разные формулы, но полученные результаты не имеют погрешностей. Чтобы провести тесты для вычисления основных параметров, используется специальное оборудование. Простые задачи с деформацией пружин решают ученики на уроках физике в 7−8 классе. О параллельном и последовательном соединении элементов системы узнают учащиеся старших классов.

Предыдущая
ФизикаЦикл Карно — формула, процессы и принципы работы
Следующая
ФизикаВлажность воздуха — способы определения, формулы и значение показателей

Лабораторная работа N06

Определение величины коэффициента жесткости пружины статическим и динамическим методами

Цель:вычислить и сравнить величины коэффициентов жесткости пружины, определенных статическим и динамическим методами.

Приборы и оборудование: штатив, набор пружин различной жесткости, набор грузов, линейка, секундомер.

Обоснование метода

1. Статический метод определения коэффициента упругости
Из закона Гука, определяющего линейную зависимость между механической деформацией тела и деформирующей силой в случае

(6.1)

ΔlFРmP=mg

(6.2)

2. Динамический метод определения коэффициента упругости
Из формулы Томсона для пружинного маятника (I.4) выразим коэффициент упругости k:

(6.3)

k_динmkT_срt_срN

(6.4)

Порядок выполнения работы

1. Соберите пружинный маятник. Для этого на штативе укрепите указанную лаборантом или преподавателем одну из пружин набора, измерив ее начальную длину в недеформированном состоянии l, и подвесьте к ней один груз известной массы m₁ из набора грузов (см. рис.5).
2. Измерьте длину пружины в растянутом (деформированном) состоянии l и определите деформацию пружины Δl=l- l.
3. Повторите измерения и расчеты еще для двух грузов массами m₂ и m₃. Вычислите по формуле (6.2) значения k_ст и рассчитайте его среднее значение k_{ст ср} по формуле (0.3) и погрешность по формуле (0.4).
4. Заполните таблицу 1.

   Таблица 1

   Результаты опыта по определению коэффициента жесткости пружины статическим методом

   Номер опыта	Масса груза m, кг	Вес груза P, Н	Длина пружины	Деформация Δl, м	kст, Н/м	kст ср ±Δkст, Н/м
   начальная l, м	после растяжения l, м
   1
   2
   3

5. Не меняя пружины, подвесьте груз массой m₁ и измерьте время t₁ для N=60 полных колебаний груза малой амплитуды.
6. Не меняя пружины и груза, повторите измерения еще 4 раза.
7. Найдите среднее время для 60 колебаний t_ср=(t₁+t₂+┘+t₅)/5 и по формуле (6.4) рассчитайте среднее значение периода колебаний T_ср.
8. По формуле (0.4) рассчитайте абсолютную Δt и по формуле (0.6) — относительную погрешность времени ε_t.
9. Используя формулу (6.3), рассчитайте среднее значение динамического коэффициента жесткости исследуемой пружины k_дин.
10. Рассчитайте относительную погрешность коэффициента упругости по формуле ε_k=2ε_t, следующей из (0.8), и по формуле (0.9) определите абсолютную погрешность Δk.
11. Заполните таблицу 2.

    Таблица 2

    Результаты опыта по определению коэффициента жесткости пружины динамическим методом

    Номер опыта	Масса груза m, кг	Число колебаний N	Время колебаний t,с	tср,с	Период Tср, с	Коэффициент упругости kдин ср, Н/м
    1
    2
    …
    5
    	Δt= ; εt=	εk= ; Δk= ;

12. Сравнив значения k_{ст ср} и k_{дин ср}, сформулируйте и запишите вывод.

Контрольные вопросы

1. Виды деформации. Закон Гука.
2. Что называется жесткостью пружины и от чего она зависит?
3. Опишите превращение энергии при колебаниях пружинного маятника.
4. Какие силы действуют на груз в опыте? Запишите закон Ньютона для него. Выведите формулу (6.2).