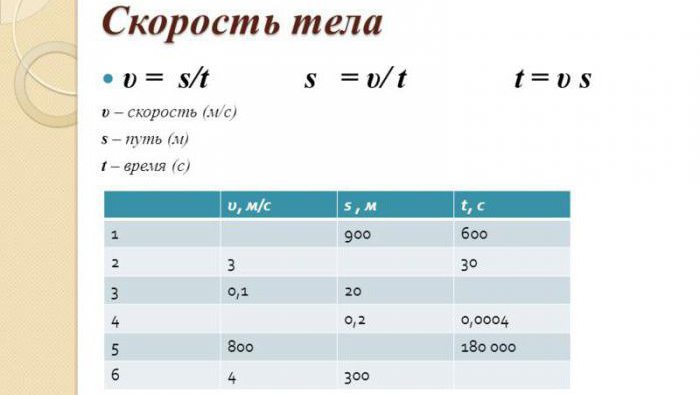
Как находить среднюю скорость
Содержание:
- Длина шага человека
- Средняя скорость бега человека
- Для чего это нужно?
- Способы вычисления среднего арифметического
- Средняя скорость при переменном движении
- Перемещение материальной точки
- Алгоритм на все случаи жизни
- Уровень B
- Максимальная скорость бега человека
- Примеры расчета среднего арифметического
- Наука и скорость бега
- Аналог «средней температуры» в механике
- Как рассчитать скорость бега
- Что влияет на скорость пешехода
- Шаги
- Формула средней скорости
- Движение по кольцевым трассам
- Как решать задачи на среднюю скорость
- Характеристика величины
- Движение по реке. Скорость течения реки
Длина шага человека
Для высчитывания средней скорости пешехода надо знать длину шага. Она зависит от таких факторов как пол, рост, раса, вес, походка (манера), и может колебаться от 30 см до 1 метра. Но определена среднестатистическая длина, для мужчины она составляет 0,76 м, а средняя длина шага женщины – 0,67 м.
Существует формула для определения средней длины шага в зависимости от роста
Дл.Ш = P:4 + 0,37
где:
Дл.Ш – длина шага (м)
P – рост.
Таким образом, средний шаг человека ростом 1,79 м составляет: Дл.Ш = 1,79 : 4 + 0,37 = 0,82 м.
Практически длину шага человека можно измерять опытным путем. Для этого необходимо отмерять участок длиной 10 метров, пройти по нему, подсчитывая количество шагов. Затем 10 м разделить на это количество, и получим длину одного.
Средняя скорость бега человека
Скорость бега зависит как от физической подготовки человека, так и от его природных данных. Первое, что влияет на скорость, – пол и возраст.
- 9-11 км/ч – средняя скорость бега ребёнка до 18 лет
- 9-12 км/ч – средняя скорость бега женщины
- 12-15 км/ч – средняя скорость бега мужчины
До пубертатного периода скорость бега мальчиков и девочек примерно одинаковая. Разрыв в цифрах начинается с момента полового созревания и обусловлен различным гормональным фоном мужчин и женщин. Поэтому к взрослому возрасту, который с точки зрения спортивных нормативов начинается с 18 лет, наблюдается ряд физиологических особенностей, объясняющих, почему женщины медленнее мужчин:
- У женщин более слабые суставы, а значит, слабее связки и сухожилия.
- Массовая доля жира в организме мужчины на 10-15% ниже, чем у женщины.
- Почти на 30% у женщин предельная сила мышц конечностей ниже, чем у мужчин.
- Объём сердца женщины меньше мужского на 10-20%.
- Женщины дольше восстанавливаются и более подвержены стрессовым реакциям.
- У женщин ниже гемоглобин, а значит организм хуже транспортирует кислород.
- У мужчин уровень тестостерона в 10 раз выше женского, то есть лучше работает опорно-двигательный аппарат.
- Каденс (шаг) женщины короче мужского.
Хотя стоит отметить, что женщины проще справляются с перепадом температур, у них лучше координация и вестибулярный аппарат.
Для чего это нужно?
Такие расчеты полезны всем. Мы все время планируем свой день и перемещения. Имея дачу за городом, есть смысл узнать среднюю путевую скорость при поездках туда.
Это упростит планирование проведения выходных. Научившись находить эту величину, мы сможем быть более пунктуальными, перестанем опаздывать.
Вернемся к примеру, предложенному в самом начале, когда часть пути автомобиль проехал с одной скоростью, а другую — с иной. Такой вид задач очень часто используется в школьной программе. Поэтому, когда ваш ребенок попросит вас помочь ему с решением подобного вопроса, вам будет просто это сделать.
Сложив длины участков пути, вы получите общее расстояние. Поделив же их значения на указанные в исходных данных скорости, можно определить время, потраченное на каждый из участков. Сложив их, получим время, потраченное на весь путь.
Ну а дальше по формуле. Объяснение кажется очень сложным, но на практике все решается в столбик за несколько минут. Попробуйте, сами в этом убедитесь.
Способы вычисления среднего арифметического
Стандартная формула. Чтобы найти среднее арифметическое, нужно сложить все числа и поделить эту сумму на их количество. Формула выглядит так:
где
- x — среднее арифметическое;
- xⁿ — конкретное значение;
- n — количество значений.
Преимущества:
- подходит при нормальном распределении значений в выборке;
- легко считать;
- интуитивно доступно.
Недостатки:
- сложно представить распределение значений;
- можно запутаться в разных величинах.
Вычисление моды или наиболее часто встречающегося значения. Формула такая:
где
- M₀ — мода;
- x₀ — нижняя граница интервала, который содержит моду;
- n — величина интервала;
- fm — частота (сколько раз в ряду встречается то или иное значение);
- fm-1 — частота интервала предшествующего модальному;
- fm+1 — частота интервала следующего за модальным.
Преимущества:
- подходит для формирования общественного мнения;
- подходит для нечисловых данных;
- доступно для понимания.
Недостатки:
- моды может не быть при отсутствии повторов;
- мод может быть несколько (многомодальное распределение).
Не обязательно быть одаренным ребенком, чтобы хватать пятерки по математике. Нейробиологи говорят, что разница только в том, с какой скоростью дети учатся: обычный ребенок может выучить все то же самое, что и одаренный, только ему потребуется больше времени и усилий.
В современной школе Skysmart верят, что математика — для всех, просто каждому нужен свой подход. Запишите ребенка на бесплатный пробный урок, чтобы начать заниматься в своем темпе, с внимательным личным учителем и в удовольствие.
Вычисление медианы, то есть значения, которое делит упорядоченную выборку на две половины и находится между ними. Если такого значения нет, за медиану принимают среднее число между границами половин выборки. Формула выглядит так:
где
- Mₑ — медиана;
- x₀ — нижняя граница интервала, который содержит медиану;
- h — величина интервала;
- f i — частота (сколько раз в ряду встречается то или иное значение);
- Sm-1 — сумма частот интервалов предшествующих медианному;
- fm — число значений в медианном интервале (его частота).
Преимущества:
- дает самую реалистичную оценку;
- устойчива к выбросам.
Недостатки:
сложнее вычислить из-за необходимости упорядочивать.
Применить эти знания можно в любой сфере жизни, где нужно обобщить и дать среднюю оценку: в магазине, на работе, в диалоге с другом или во время презентации перед инвесторами. Еще пригодятся, чтобы рассчитать среднюю скорость движения.
Средняя скорость движения — это весь пройденный путь, поделенный на время движения. Формула:
Так мы рассмотрели самые основные методы нахождения среднего значения. Теперь осталось попрактиковаться на примерах, чтобы быстро решать задачки на контрольной.
Средняя скорость при переменном движении
При неравномерном движении величина средней скорости сильно зависит от выбора промежутка времени движения тела.
Рассмотрим движение тела, которое свободно падает вниз. Закон движения при этом:
Для моментов времени $t_1=0,1\ $c координата тела (подставим время $t_1$ в формулу (4)) равна: $x_1=0,049\ $м; для $t_2=0,2\ $c$\ x_2=0,196$ м, тогда $\left\langle v\right\rangle $в промежутке времени от $t_1=0,1$ с до $t_2=0,2\ $c будет:
Если взять для того же свободно падающего тела промежуток времени от $t_1=0,7$ с до $t_2=0,8\ $c, то средняя скорость получится равной $\left\langle v\right\rangle =7,4\frac$.
Перемещение материальной точки
Пусть материальная точка совершает движение по оси X все время в одном направлении. Тогда перемещением этой материальной точки за отрезок времени $\Delta t=t_2-t_1$ будет отрезок $\Delta x=x_2-x_1$. Если материальная точка все время своего движения перемещалась в одном направлении, то пройденный путь ($\Delta s$) равен по модулю величине перемещения:
\
Если точка движется сначала в одном направлении, затем останавливается и движется в противоположном направлении, (например, так движется тело брошенное вертикально вверх) то путь равен сумме модулей перемещений в обоих направлениях:
\
Алгоритм на все случаи жизни
Для того чтобы наверняка избежать ошибки, при решении вопроса, как найти среднюю скорость, достаточно запомнить и выполнить простую последовательность действий:
- определить весь путь, просуммировав длины отдельных его участков;
- установить всё время пути;
- поделить первый результат на второй, неизвестные, не заданные в задаче величины при этом (при условии корректной формулировки условий) сокращаются.
В статье рассмотрены простейшие случаи, когда исходные данные приводятся для равных долей времени или равных участков пути. В общем случае соотношение хронологических промежутков либо пройденных телом расстояний может быть самым произвольным (но при этом математически определённым, выраженным конкретным целым числом или дробью). Правило обращения к соотношению vср = S : t абсолютно универсально и никогда не подводит, сколь бы сложные на первый взгляд алгебраические преобразования ни приходилось выполнять.
Напоследок отметим: для наблюдательных читателей не осталась незамеченной практическая значимость использования верного алгоритма. Правильно рассчитанная средняя скорость в приведённых примерах оказалась несколько ниже «средней температуры» на трассе. Поэтому ложный алгоритм для систем, фиксирующих превышения скорости, означал бы большее число ошибочных постановлений ГИБДД, высылаемых в «письмах счастья» водителям.
Уровень B
1. О какой скорости – средней или мгновенной – идет речь в следующих случаях:
а) пуля вылетает из винтовки со скоростью 800 м/с;
б) скорость движения Земли вокруг Солнца 30 км/с;
в) на участке дороги установлен ограничитель максимальной скорости – 60 км/ч;
г) мимо вас проехал автомобиль со скоростью 72 км/ч;
д) автобус преодолел расстояние между Могилевом и Минском со скоростью 50 км/ч?
2. Путь в 63 км от одной станции до другой электропоезд проходит за 1 ч 10 мин со средней скоростью 70 км/ч. Какое время занимают остановки?
3. Самоходная косилка имеет ширину захвата 10 м. Определите площадь поля, скошенного за 10 мин, если средняя скорость косилки 0,1 м/с.
4. На горизонтальном участке пути автомобиль ехал со скоростью 72 км/ч в течение 10 мин, а затем проехал подъем со скоростью 36 км/ч за 20 мин. Чему равна средняя скорость на всем пути?
5. Велосипедист первую половину времени при переезде из одного пункта в другой ехал со скоростью 12 км/ч, а вторую половину времени (из-за прокола шины) шел пешком со скоростью 4 км/ч. Определите среднюю скорость движения велосипедиста.
6. Школьник проехал 1/3 всего времени на автобусе со скоростью 60 км/ч, еще 1/3 всего времени на велосипеде со скоростью 20 км/ч, остальное время прошел со скоростью 7 км/ч. Определите среднюю скорость движения школьника.
7. Велосипедист ехал из одного города в другой. Половину пути он проехал со скоростью 12 км/ч, а вторую половину (из-за прокола шины) шел пешком со скоростью 4 км/ч. Определите среднюю скорость его движения.
8. Из одного пункта в другой мотоциклист двигался со скоростью 60 км/ч, обратный путь им был пройден со скоростью 10 м/с. Определите среднюю скорость мотоциклиста за все время движения.
9. Школьник проехал 1/3 пути на автобусе со скоростью 40 км/ч, еще 1/3 пути на велосипеде со скоростью 20 км/ч, последнюю треть пути прошел со скоростью 10 км/ч. Определите среднюю скорость движения школьника.
10. Пешеход часть пути прошел со скоростью 3 км/ч, затратив на это 2/3 времени своего движения. Оставшееся время он прошел со скоростью 6 км/ч. Определите среднюю скорость.
11. Скорость поезда на подъеме 30 км/ч, а на спуске – 90 км/ч. Определите среднюю скорость на вcем участке пути, если спуск в два раза длиннее подъема.
12. Половину времени при переезде из одного пункта в другой автомобиль двигался с постоянной скоростью 60 км/ч. С какой постоянной скоростью он должен двигаться оставшееся время, если средняя скорость движения равна 65 км/ч?
Максимальная скорость бега человека
Следующий фактор, который влияет на скорость, – дистанция. Большинство тренированных людей могут бежать со скоростью 15-20 км/ч, но не более одного километра. Дальше их скорость начнёт падать до 12-15 км/ч. Если говорить об элитных спортсменах, то на марафонских дистанциях скорость мужчин составляет 19-21 км/ч. Женские показатели в беге на 12-15% ниже.
Учитывая дистанцию, бегуны делятся на спринтеров (100-400 м), средневиков (800-3000 м), стайеров (5000-10000 м) и марафонцев, и системы их тренировок кардинально отличаются.
Самые высокие показатели скорости характерны для спринтерских дистанций: лучшие спортсмены преодолевают 100-метровку за 10-11 секунд, а 200 м за 19-20 секунд. Такое время спортсмены показывают в основном на соревнованиях, потому что даже на тренировках их скорость на 10-20% ниже максимальной.
У стайеров и марафонцев на первом плане – выносливость, способность держать стабильную скорость на протяжении длительного времени и разогнаться к финишу. У новичков на длинных дистанциях скорость составляет 9-12 км/ч, у тренированных людей – 16-18 км/ч.
Читайте по теме: Как развить и увеличить выносливость в беге
Быстрее всех пробежал 42 км 195 м Элиуд Кипчоге в октябре 2019 года – за 1 час 59 минут и 40,2 секунды. Для этого ему пришлось бежать всю дистанцию, сохраняя скорость 21,1 км/ч. Но этот рекорд не был засчитан, поскольку условия забега были почти “лабораторными” и нарушали марафонские правила.
Действующий мировой рекорд установил он же в 2018 году на марафоне в Берлине, пробежав его за 2 часа 1 минуту и 39 секунд.
Неоднократно спринтеров и стайеров пытались сравнить, и для этого учёные вычислили дистанцию, на которой их физическая форма может быть сопоставима – это 492 метра.
Для интереса можно взглянуть, как марафонец-любитель Искандер Ядгаров и спринтер-профессионал Рушан Абдулкадеров в 2018 году выясняли, кто из них будет быстрее на дистанции 450 м.
Примеры расчета среднего арифметического
Пример 1. Вычислить среднее арифметическое 33,3 и 55,5.
Как решаем:
Чтобы найти среднее арифметическое двух чисел, надо сложить эти числа и результат разделить на 2: (33,3 + 55,5) : 2 = 88,8 : 2 = 44,4.
Пример 2. Посчитать среднее арифметическое 7,5 и 8 и 0,5.
Как решаем:
Чтобы найти среднее арифметическое трех чисел, надо сложить эти числа и результат разделить на 3: (7,5 + 8 + 0,5) : 3 = 16 : 3 = 5,33.
Пример 3. Найти среднее арифметическое 202, 105, 67 и 9.
Как решаем:
Чтобы найти среднее арифметическое трех чисел, надо сложить эти числа и результат разделить на 4: (202 + 105 + 67 + 9) : 4 = 383 : 4 = 95,75.
Пример 4. Сколько в среднем тратит школьник денег в неделю, если в понедельник он потратил 80 рублей, во вторник 75 рублей, в среду и четверг по 100 рублей, в пятницу 50 рублей.
Как решаем:
Чтобы найти сколько в среднем школьник потратил за пять дней, надо сложить эти суммы и результат разделить на 5: (80 + 75 + 100 + 100 + 50) : 5 = 405 : 5 = 81.
Ответ: школьник в неделю тратит в среднем 81 рубль.
В 5 классе можно искать среднее арифметическое с помощью онлайн-калькулятора. Пользуйтесь им, если уже разобрались с темой и щелкаете задачки легко и без помощников:
- Калькулятор раз
- Два
- Три
Наука и скорость бега
Ученые утверждают, что человек способен бежать со скоростью почти 65 км/ч. Новое исследование американских учёных о биологических пределах скорости предлагает по-новому посмотреть на биологию скорости человека.
Считается, что скорость ограничена силой, с которой конечности могут ударяться о поверхность во время бега. Элитные спортсмены могут прикладывать от 360 до 456 кг на одну конечность во время каждого шага. С такими цифрами легко поверить, что они бегут на пике своих возможностей. Но учёные выяснили, что это не так. Что конечности способны прикладывать гораздо большие силы к поверхности.
Ответ кроется в периодах времени контакта стопы с землёй. У элитных спринтеров это время составляет менее одной десятой секунды, а пиковые значения составляют менее одной двадцатой секунды.
Для исследования учёные использовали высокоскоростную беговую дорожку, развивающую скорость более 65 км/ч и способную измерять силу каждого шага. На ней спортсмены бежали назад, вперёд, прыгали на одной ноге. Оказалось, что во время прыжков на одной ноге на максимальной скорости сила, приложенная к поверхности, больше силы при беге на максимальной скорости на двух ногах на 30%.
Также выяснилось, что время соприкосновения ноги с поверхностью при беге вперёд совпадает во временем соприкосновения конечности при беге назад, при этом бег назад, конечно, медленнее. Это совпадение времени при двух очень разных видах активности указывает, насколько быстро мышечные волокна могут создавать силы, необходимые для того, чтобы бегун отрывался от земли во время каждого шага.
Новая работа показывает, что ограничения скорости бега устанавливаются ограничениями скорости сокращения самих мышечных волокон, а скорость сокращения волокон устанавливает предел того, насколько быстро конечность бегуна может прикладывать силу к поверхности бега.
Чтобы преодолеть биологические ограничения скорости, учёные из Гарварда придумали экзокостюм, который снижает метаболические затраты на бег и повышает мышечную производительность. Этот костюм лёгкий и плотно облегает тело. Он имеет приводной блок, который тянет за провода, выступающие в роли второй пары мышц-разгибателей бедра. Исследование показало, что помогая мышцам бедра, костюм влияет и на разгибание колена, и на прикладываемую ступнёй силу к поверхности.
На данный момент исследования продолжаются, чтобы ещё больше снизить метаболические затраты на бег. Еще один немаловажный аспект – доступность такого экзокостюма. Цель учёных – разработать портативную систему, чтобы польза от неё значительно снижала стоимость её ношения.
Есть версия, что скорость бега человека ограничена, потому что большую часть времени бега мы находимся в воздухе. А когда наши ноги касаются земли, у нас остается слишком мало времени, чтобы приложить силу к поверхности. Так, Усэйн Болт находится на земле 42-43% от общего времени шага, в то время как самые быстрые животные – гепард или лошадь – тратят две трети времени шага на контакт с землёй. Неужели, чтобы бежать быстрее, стоит бежать на четырех ногах?
Мировой рекорд Гиннесса для человека, бегущего 100 метров на четвереньках, улучшился с 18,58 секунды в 2008 году (первый год отслеживания записи) до 15,71 секунды в 2015 году. Исследователи сделали вывод на основе этих цифр, что к 2048 году человек на четвереньках сможет двигаться быстрее, чем человек, бегущий прямо!
Аналог «средней температуры» в механике
В каких случаях каверзно сформулированные условия задачи подталкивают нас к поспешному необдуманному ответу? Если говорится о «частях» пути, но не указывается их протяжённость, это настораживает даже мало искушённого в решении подобных примеров человека. А вот если в задаче прямо указывается на равные промежутки, например, «первую половину пути поезд следовал со скоростью…», или «первую треть пути пешеход прошагал соскоростью…», и далее подробно расписывается, как объёкт передвигался на оставшихся равных участках, то есть известно соотношение S1 = S2 = … = Sn и точные значения скоростей v1, v2, … vn, наше мышление нередко даёт непростительную осечку. Считается среднее арифметическое скоростей, то есть все известные значения vскладываются и делятся на n. В итоге ответ получается неверный.

Как рассчитать скорость бега
Скорость показывает, какое расстояние вы преодолеваете в единицу времени. Может измеряться в метрах в секунду или в километрах в час.
Скорость – первый критерий, главная мера для бегунов. Даже несмотря на то, что спортивные часы чаще фиксируют наш темп, чем скорость. При этом темп (pace) – величина, обратная скорости (speed). Темп измеряется в минутах на километр и показывает, сколько времени тратит человека на преодоление определенного расстояния.
Формула расчёта скорости:
Скорость (км/ч) = (расстояние/время в минутах)*60
Темп (мин/км) = время в минутах/расстояние
Формула расчёта скорости из показателя темпа:
Следите за новостями из мира бега в нашем телеграм-канале Бегущая строка.
Пишем коротко и по делу.
Скорость = 60/темп (км/ч) или 50/3*темп (м/с)
Что влияет на скорость пешехода
Скорость пешехода зависит от множества факторов. Вот некоторые из них:
- возраст — маленькие дети и люди преклонных лет ходят намного медленнее, нежели обычный трудоспособный человек
- физическая подготовка и состояние здоровья пешехода
- удобство одежды и обуви. Надеюсь, никто не станет спорить с тем, что женщина на высоких каблуках и женщина в кроссовках будут передвигаться с кардинально разной скоростью
- качество покрытия дороги, по которой идет человек;
- скорость изменяется от того, двигается человек по пересеченной местности или по тротуару
- ученые отмечают, что скорость жителей густонаселенных пунктов ниже, нежели тех, кто передвигается по безлюдной местности.
Шаги
Метод 1 из 2:
Часть 1: Определение средней скорости изменения функции
-
1
Функция. Это соответствие между переменными величинами, в котором каждому значению некоторой независимой переменной «x» соответствует определенное значение зависимой переменной «у».
-
2
Переменная. Это величина, в процессе своего изменения принимающая различные значения. Переменные, как правило, обозначаются через «х» и «у».
-
3
Угловой коэффициент. Он равен тангенсу угла между положительным направлением оси абсцисс и данной прямой линией. Угловой коэффициент характеризует скорость изменения линейной функции.
-
4
Секущая. Это прямая, пересекающая две или более точки, лежащих на кривой. При вычислении средней скорости изменения функции вы находите угловой коэффициент секущей между двумя заданными точками.
-
5
Основная формула для вычисления средней скорости изменения функции показана на рисунке.
Метод 2 из 2:
Часть 2: Вычисление средней скорости изменения функции
-
1
Найдите f(x + h).
Вычислите f(x + h), используя следующее выражение: f(x + h) = (х + h)^2 = x^2 + 2xh + h^2.
В исходной функции f(x) замените «х» на «x + h», где h – приращение аргумента (то есть изменение независимой переменной «х»).Например, дана функция f(х) = x^2. Вычислите среднюю скорость изменения функции между в интервале (2,5) (то есть х1 = 2 и х2 = 5).
-
2
Вычислите среднюю скорость изменения, воспользовавшись основной формулой и подставив в нее исходную функцию f(x) и преобразованную функцию f(x+h).
В приведенном выше примере вычисления показаны на рисунке.
WH.shared.addScrollLoadItem(‘cc51182fbff452ca00cb398923769107’){«smallUrl»:»https:\/\/www.wikihow.com\/images_en\/thumb\/e\/e7\/Screen-Shot-2014-03-11-at-5.00.07-PM.png\/460px-Screen-Shot-2014-03-11-at-5.00.07-PM.png»,»bigUrl»:»https:\/\/www.wikihow.com\/images\/thumb\/e\/e7\/Screen-Shot-2014-03-11-at-5.00.07-PM.png\/728px-Screen-Shot-2014-03-11-at-5.00.07-PM.png»,»smallWidth»:460,»smallHeight»:111,»bigWidth»:»728″,»bigHeight»:»176″,»licensing»:»
«}
-
3
Найдите h.
В приведенном выше примере: h = x2 — x1 = 5 — 2 = 3.
Для этого вычтите начальное значение переменной «х» из ее конечного значения. Другими словами, если интервал задается в виде (x1, x2), то h = x2 — x1.
-
4
Вычислите среднюю скорость изменения.
В приведенном выше примере: А(х) = 2х + h = 2 × 2 + 3 = 7
Поставьте найденное значение h в выведенную выше формулу (вместо «х» подставьте значение x1).
-
5
Запишите ответ. В нашем примере средняя скорость изменения функции равна 7.
Формула средней скорости
Средняя скорость тела – это отношение пути к времени прохождения этого пути. Скорость движения не требуется постоянной.
Здесь – средняя скорость, – весь путь, пройденный телом, – время прохождения пути.
Единица измерения скорости – м / с (метр в секунду).
Средняя скорость – это скаляр. Если тело перемещается с разной скоростью в равные промежутки времени, то средняя скорость равна среднему арифметическому для всех скоростей, в противном случае
Где – отрезок пути, – время прохождения этого отрезка.
Примеры решения проблем на тему «Средняя скорость»
Тело прошло 5 метров за 12 секунд, затем 7 метров за 3 секунды. Найдите среднюю скорость тела.
Решение очевидно (S и t – путь и время прохождения этого пути для определенных сегментов):
Средняя скорость тела равна метров в секунду.
Средняя скорость движения тела . Скорость на первой секции была , на второй , на третьей длине секций S1, S2 и S3 соответственно. Мы не знаем S2. Найдите время прохождения второго раздела.
Давайте рассмотрим формулу средней скорости для трех разделов:
В этой форме формула ничего нам не дает, но если вспомнить, что
Источник статьи: http://sciterm.ru/spravochnik/formula-srednej-skorosti/
Движение по кольцевым трассам
Задача 6. (www.reshuege.ru) Из пункта A круговой трассы длиной 46 км выехал велосипедист, а через 20 минут из пункта A следом за велосипедистом отправился мотоциклист. Через 5 минут после отправления мотоциклист догнал велосипедиста в первый раз, а еще через 46 минут после этого мотоциклист догнал велосипедиста во второй раз. Найдите скорости велосипедиста и мотоциклиста.
Решение. К тому моменту, когда мотоциклист в первый раз догнал велосипедиста, мотоциклист ехал 5 минут, а велосипедист ехал 25 минут, причем проехали они один и тот же путь. Отсюда вытекает, что скорость мотоциклиста в 5 раз больше скорости велосипедиста.
Таким образом, обозначив буквой v (км/час) скорость велосипедиста, получаем, что скорость мотоциклиста равна 5v (км/час).
В условии задачи дано время, прошедшее между двумя последовательными встречами мотоциклиста и велосипедиста, – 46 минут. Это время необходимо выразить в часах, чтобы все единицы измерения были согласованными:
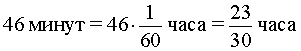
Изобразим данные задачи, касающиеся движения мотоциклиста и велосипедиста между первой и второй встречами, на рисунке 6.
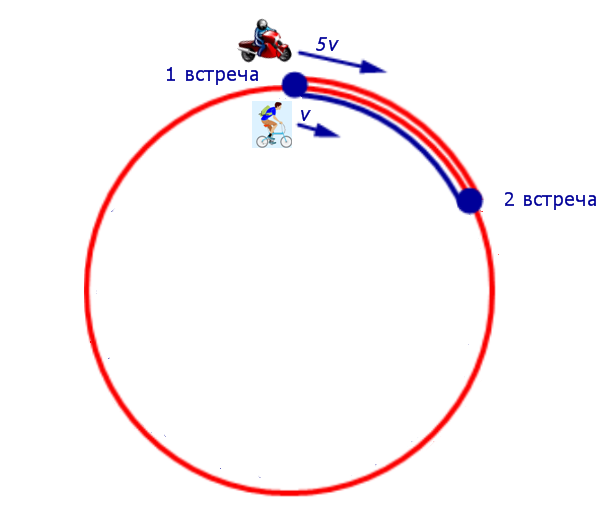
Рис. 6
Поскольку за время часа, прошедшее от момента первой встречи до момента второй встречи, мотоциклист проехал 46 км (вся круговая трасса) плюс путь, который проехал велосипедист за часа, то можно составить следующее уравнение:
Решая это уравнение, находим скорость велосипедиста:
v = 15 .
Ответ. Скорость велосипедиста 15 км/час, скорость мотоциклиста 75 км/час.
Задача 7. На дороге, представляющей собой окружность длиной 60 км, пункты A и B являются диаметрально противоположными точками. Велосипедист выехал из пункта A и сделал два круга. Первый круг он прошел с постоянной скоростью, после чего уменьшил скорость на 5 км/час. Время между двумя прохождениями велосипедиста через пункт B равно 5 часам. Найти скорость, с которой велосипедист прошел первый круг.
Решение. Для определенности будем считать, что велосипедист двигался по кругу по часовой стрелке и рассмотрим рисунок 7.
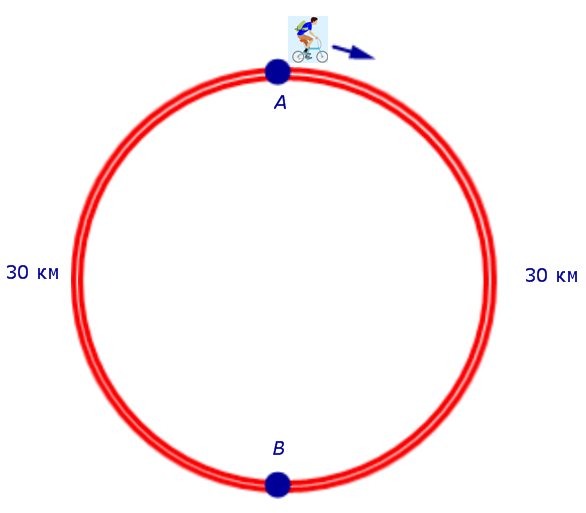
Рис. 7
Если обозначить буквой v (км/час) скорость, с которой велосипедист прошел первый круг, то скорость велосипедиста на втором круге будет равна v – 5 (км/час), и можно составить уравнение
Решая это уравнение, находим скорость велосипедиста на первом круге:
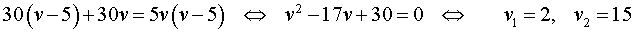
Поскольку скорость велосипедиста на первом круге больше, чем 5 км/час, то первый корень должен быть отброшен.
Ответ. 15 км/час.

Желающие ознакомиться с примерами решения различных задач по теме «Проценты» и применением процентов в экономике и финансовой математике могут посмотреть разделы нашего справочника «Проценты. Решение задач на проценты», «Простые и сложные проценты. Предоставление кредитов на основе процентной ставки», а также наши учебные пособия «Задачи на проценты» и «Финансовая математика».
Приемы, используемые для решения задач на выполнение работ представлены в разделе нашего справочника «Задачи на выполнение работ».
С примерами решения задач на смеси, сплавы и растворы можно ознакомиться в разделе нашего справочника «Задачи на смеси, сплавы и растворы».
Как решать задачи на среднюю скорость
В ЕГЭ по матматике профильного уровня встречаются задачи на нахождение средней скорости автомобиля, путешественника, бегуна и т.п. В этой статье мы постараемся разобраться со способами решения данного типа зданий. Попробуйте решить следующие задачи:
- Первую треть трассы велосипедист ехал со скоростью 12 км/ч, вторую треть – со скоростью 16 км/ч, а последнюю треть – со скоростью 24 км/ч. Найдите среднюю скорость велосипедиста на протяжении всего пути. Ответ дайте в км/ч.
- Путешественник переплыл море на яхте со средней скоростью 20 км/ч. Обратно он летел на спортивном самолете со скоростью 480 км/ч. Найдите среднюю скорость путешественника на протяжении всего пути. Ответ дайте в км/ч.
- Половину времени, затраченного на дорогу, автомобиль ехал со скоростью 74 км/ч, а вторую половину времени – со скоростью 66 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути. Ответ дайте в км/ч.
Если у Вас возникает недопонимание, или же вы просто не знаете как решать такие задачи, то данная статья предназначена как раз для Вас!
Средняя скорость объекта
Для начала вспомним формулу, по которой решаются все задачи на движение: \( S=vt \) — пройденный путь равняется произведению скорости и времени. Так вот, средняя скорость равна отношению всего пути ко времени, которое было затрачено на прохождение этого пути. Если перевести на математический язык:
\
Однако, раз возникла нужда вычислить среднюю скорость, то наверняка она была разной на различных промежутках. Например, Вам необходимо прийти в школу. Сначала вы какой-то путь проезжаете на автобусе, а затем идете пешком.
Условно, весь ваш путь можно разделить на 2 промежутка, и на обоих Ваша скорость и время его прохождения будет разной.
Аналогично мы должны вычислить и общее время, которое было затрачено на прохождение всего пути. То есть \( t=t_1+t_2+\ldots+t_n \), причем время вычисляем на каждом промежутке! То есть, запишем математически формулу для нахождения времени на n-м промежутке: \( t_n=\dfrac{S_n}{v_n} \)
Решение задач
А теперь, обогатившись некоторой теорией решим первую из предложенных задач:
Первую треть трассы велосипедист ехал со скоростью 12 км/ч, вторую треть – со скоростью 16 км/ч, а последнюю треть – со скоростью 24 км/ч. Найдите среднюю скорость велосипедиста на протяжении всего пути. Ответ дайте в км/ч.
Решение:
- По условию задачи мы видим, что автомобиль прошёл сначала одну треть, затем вторую треть и последнюю треть. Значит весь его маршрут состоит из трёх участков. Поэтому удобно обозначить длину всего его пути за \( 3S \)
- Теперь нам необходимо выяснить за какое время автомобиль прошёл каждый из этих промежутков (воспользовавшись формулой \( t_n=S_n/v_n \)). Причем длина каждого из трёх промежутков будет равна S.
- Время, за который был пройдена первая треть: \( t_1=\dfrac{S}{12} \).
- Аналогично, найдем время, за которое были пройдены вторая и третья трети всего пути: \( t_2=\dfrac{S}{16} \) и \( t_3=\dfrac{S}{24} \)
- Итак, мы выяснили сколько времени тратит автомобиль на прохождение каждого из отрезков своего пути, значит можем найти сколько он потратил времени всего: \( t=t_1+t_2+t_3 \). Таким образом: \( t=\dfrac{9S}{48} \)
Теперь мы знаем длину всего пути (\( 3S \)) и сколько времени автомобиль затратил на прохождение всего пути (\( t=\dfrac{9S}{48} \), значит найти среднюю скорость не составит и труда:
\
Ответ: 16
Теперь постарайтесь самостоятельно решить оставшиеся две текстовые задачи на нахождение средней скорости, а если не получается, то посмотрите видео-урок
-урок: «Как решать задачу на нахождение средней скорости»:
В данном видео-уроке я покажу, как решаются все три предложенные текстовые задачи на нахождение средней скорости. Также Вы можете сравнить своё решение с моим.
- #6. Длина хорды
- Как готовиться к ЕГЭ по математике самостоятельно (часть 1)
Характеристика величины
Скорость в физике — это величина, описывающая количество пути, пройденного за единицу времени. То есть когда говорят, что скорость пешехода составляет 5 км/ч, это означает, что он проходит расстояние в 5 км за 1 час.
Единой размерности в этой формуле нет, поскольку с ее помощью описываются и крайне медленные, и очень быстрые процессы.
Например, искусственный спутник Земли преодолевает порядка 8 км за 1 секунду, а тектонические плиты, на которых расположены материки, по измерениям ученых, расходятся всего на несколько миллиметров за год. Поэтому и размерности у скорости могут быть разными — км/ч, м/с, мм/с и т.д.
Принцип заключается в том, что расстояние делится на время, необходимое для преодоления пути. Не стоит забывать о размерности, если проводятся сложные расчеты.
Чтобы не запутаться и не ошибиться в ответе, все величины приводятся в одни и те же единицы измерения. Если длина пути указана в километрах, а какая-то его часть в сантиметрах, то, пока мы не получим единства в размерности, правильного ответа нам не узнать.
Движение по реке. Скорость течения реки
В отличие от задач на движение по суше, в задачах на движение по реке появляется новая величина – скорость течения реки.
По отношению к берегу, который неподвижен, скорость тела, движущегося по течению реки, равна сумме собственной скорости тела (скорости тела по озеру, скорости тела в неподвижной воде, скорости тела в стоячей воде) и скорости течения реки. По отношению к берегу скорость тела, движущегося против течения реки, равна разности собственной скорости тела и скорости течения реки.
Задача 4. Моторная лодка прошла по течению реки 14 км, а затем 9 км против течения, затратив на весь путь 5 часов. Скорость лодки в стоячей воде 5 км/час. Найдите скорость течения реки.
Решение. Обозначим буквой v скорость течения реки и будем считать, что скорость v измеряется в км/час.Изобразим данные, приведенные в условии задачи 4, на рисунке 3.
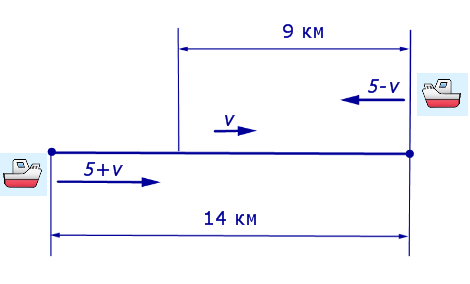
Рис. 3
Тогда
5 + v – скорость, с которой лодка шла по течению реки (в км/час);
– время движения лодки по течению реки (в часах);
5 – v – скорость, с которой лодка шла против течения реки (в км/час);
– время движения лодки против течения реки (в часах);
Теперь можно составить уравнение, принимая во внимание тот факт, что лодка находилась в пути 5 часов:
Решим это уравнение:
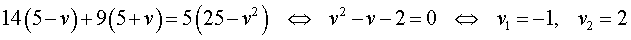
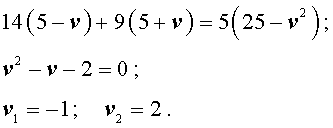
По смыслу задачи первый корень должен быть отброшен.
Ответ. 2 км/час.
Задача 5. (Бюро «Квантум») Моторная лодка прошла по течению реки 34 км и 39 км против течения, затратив на это столько же времени, сколько ей нужно, чтобы пройти 75 километров в стоячей воде. Найдите отношение скорости лодки в стоячей воде к скорости течения реки.
Решение. Обозначим vс (км/ч) скорость лодки в стоячей воде и обозначим vр (км/ч) скорость течения реки. Изобразим данные задачи 5 на рисунках 4 и 5.
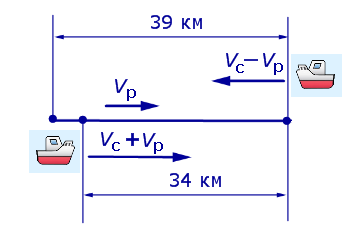
Рис. 4
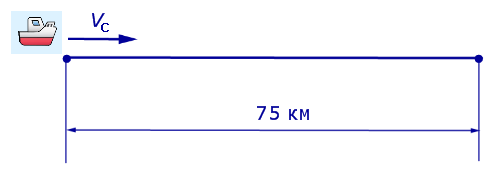
Рис. 5
Учитывая тот факт, что в обеих ситуациях лодка провела в пути одно и то же время, можно составить уравнение:
| (3) |
Если ввести обозначение
то, воспользовавшись формулой
vс = xvр ,
перепишем уравнение (3) в виде
| (4) |
Умножая уравнение (4) на vр , получим
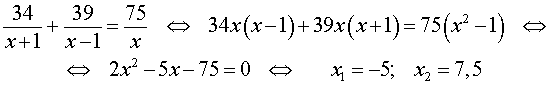
По смыслу задачи первый корень должен быть отброшен.
Ответ. 7,5 .